| Статья для энциклопедии "Наглядная арифметика" (автор В.Б. Творогов, 2013) |
Наглядная арифметика
как раздел математики
Наглядная арифметика - раздел математики, который изучает арифметику средствами геометрии.
В задачи наглядной арифметики входит изучение геометрических преобразований, с помощью которых можно отобразить (визуализировать) алгоритмы устного счёта на геометрических схемах.
Наглядная арифметика строится на системе стандартов и соглашений, позволяющих разным людям одинаково понимать геометрические схемы, реализующие цифровые правила. Важнейшие стандарты - это числовая линия и телефонная Т-матрица.
Наглядная арифметика
как совокупность визуальных образов
Неформальный термин "наглядная арифметика" часто используется в методиках обучения. Он представляет собой совокупность наглядных образов для демонстрации свойств чисел и действий с ними.
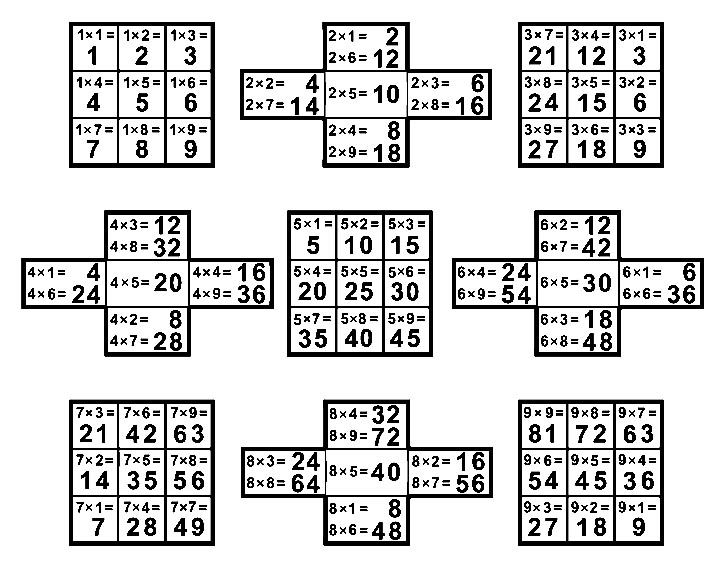
Так, навыки сложения принято формировать у детей с помощью счётных палочек, камешков и пересчитываемых предметов. Более сложные примеры организации элементов можно видеть в квадратной таблице умножения Пифагора.
Интересные способы получения цифр произведения множителей дают цифровые вертушки на телефонной Т-матрице, использующие принцип поворота.
Технология устного счёта - это совокупность навыков и знаний о числах, позволяющих человеку считать без записи промежуточных результатов на бумаге или других носителях информации.
Выделим три вида технологии устного счёта, которые используют различные физические возможности человека:
- счёт "на пальцах";
- аудиомоторная технология устного счёта;
- визуальная технология устного счёта.
В одном алгоритме расчёта человек может использовать элементы всех трех базовых технологий вычислений. Отдельные фрагменты вычислений дублируются разными средствами, так как, например, о визуальном образе можно рассказать словами.
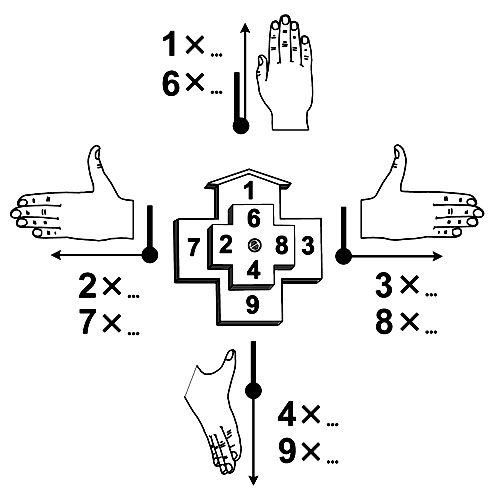
Счёт "на пальцах" является системой навыков, позволяющих подсчитать небольшое количество предметов. Этот способ счёта базируется на принципе установления взаимно однозначного соответствия подсчитываемых предметов и пальцев на руках. На руке человека пять пальцев, а рук две, поэтому образуется десять эталонных объектов – пальцев, которые можно пронумеровать по порядку. Пальцы на руках, используемые как единицы счёта, упорядочены в линию. При устном счёте можно загибать или, напротив, разгибать пальцы рук, отмечая новое однозначное число. Способ последовательного сопоставления объектов и пальцев является надежным, но чрезвычайно медленным. Недостатком этого «механического» способа счёта является сложность работы с многозначными числами. Используя счёт на пальцах, затруднительно проводить умножение и деление даже в пределах до сотни.
Аудиомоторная технология устного счёта характеризуется тем, что каждое число и каждое действие сопровождается словесной фразой типа «Дважды два – четыре». Традиционная технология устного счёта является именно аудиомоторной технологией. Современная система обучения арифметике построена на словесном объяснении исходного состояния, действий и результатов, сопровождающих устный счёт. Попросите человека дать ответ примера умножения « 7 x 8 = ? ». Вы услышите фразу «Семью восемь равно пятьдесят шесть». Как «решен» данный пример « 7 x 8 » ? Человек сформулировал некоторую стандартную фразу об исходных данных умножения – множителях 7 и 8: «Семью восемь …». Он произносит начало этой фразы. Подключается аудиопамять человека, которая продолжает эту заученную фразу, как мелодию песни. По памяти воссоздаётся словесное выражение «…пятьдесят шесть». Когда аудиофраза завершается, человек распознаёт прозвучавшую в сознании фразу как числовой ответ, который можно записать цифрами.
Умножение двух однозначных чисел занимает время около секунды, что показывает характерную скорость одного шага вербального устного счёта. В многошаговых алгоритмах расчётов выстраивается длинная цепь словесных фраз, сопровождающих вычисления. Умножение двузначных чисел представляет собой алгоритм из нескольких действий, реализующий поразрядной умножение и сложение. У человека обычных способностей такое вычисление занимает время до десяти секунд.
Скажем несколько слов о недостатках аудиоспособа запоминания:
- отсутствие в запоминаемой фразе взаимосвязей с соседними результатами,
- невозможность выделить отдельно десятки и единицы ответа без повторения всей фразы,
- невозможность обратить фразу вспять от ответа к множителям, что важно для выполнения деления с остатком,
- низкая скорость воспроизведения словесной фразы.
Супервычислители поражают наше воображение, показывая колоссальные способности мышления человека. Как они считают? Детали этого процесса скоростного вычисления не вполне известны, по крайней мере, современная педагогика до сих пор не могла научить людей быстрому счёту. Несомненно, супервычислители используют свои визуальные возможности и отличную зрительную память для определения ответа. Люди, которые владеют скоростными вычислениями, не используют слов в процессе решения арифметического примера в уме. Супервычислители запоминают большое количество вспомогательных таблиц. Многие из них помнят таблицу умножения двузначных чисел в пределах до 100. Повышению скорости счёта им помогают различные способы сокращенных вычислений.
Феноменальные счётчики неопровержимо доказывают, что технология визуального счёта существует и доступна для психофизического склада человека.
Наша задача состоит в том, чтобы исследовать визуальную технологию устного счёта методами геометрии.
Исходное пространство
Идея №1 в организации визуальных элементов счёта очевидна и используется с древних времен. Человек представляет себе числа в виде конфигураций элементов (устойчивых геометрических структур). Свойства конфигураций используются в устных вычислениях, заменяя числовые расчёты геометрическими построениями. Простейшие конфигурации "гантель" 1+1=2 , "квадрат" 2+2=4 , пальцы одной руки - это 5. Тогда 5+5=10 - сумма пальцев на двух руках. С этих конфигураций начинает изучение арифметики каждый ребенок.
Визуальная технология устного счёта опирается на геометрические представления и имеет теоретическое обоснование в рамках наглядной арифметики.
На плоскости применяется конфигурации, упорядочивающие цифры несколькими способами. Известны: телефонная "Т-матрица 3x3" = 9 элементов, "квадрат с центром" = 5 элементов и др. Многие конфигурации используют центральные и осевые симметрии: вспомним метки на гранях игральных кубиков. Важнейшими являются базовые конфигурации, в которых элементы нумерованы, это - элементы в ряд, цифры Т-матрицы размерами 3x3, полные десятки (базовые числа).
Кажущееся многообразие при выборе полезных для счёта конфигураций обманчиво. Ограничения, требующие линейности нумераций (линейные пространства) и сохранения симметрий поворотов на плоскости оставляют только два приемлемых для устного счёта пространства. В теории наглядной арифметики доказано, что годятся - числовая линия с целочисленными метками и числовая плоскость, продолжающая структурные правила Т-матрицы: "шаг направо" - это плюс 1, шаг вниз - это плюс 3.
Обозначим две целочисленные координаты точки на плоскости (X;Y). Целочисленные точки плоскости (X;Y) можно пронумеровать, используя функцию нумерации N(X;Y) = X + 3Y. Получим числовую плоскость, на которой точкам с целочисленными координатами приписаны целые числа.
Существует математический прием "склейки точек", который позволяет получить из числовой плоскости Т-матрицу. Чтобы на плоскости из ее чисел возникла Т-матрица, но не её зеркальный аналог, нужно, чтобы первая координата X отсчитывалась направо (+1), а вторая координата Y отсчитывалась от начала координат вниз (здесь действует правило "шаг вниз" = (сложение +3)).
После нумерации сотрем все цифры в разрядах десятков и старше. Останутся только цифры единиц. В результате склейки точек с одинаковыми единицами в номерах, получим цифровую плоскость.
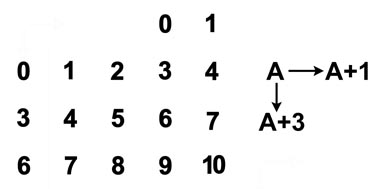
Примем соглашение о том, что все одинаковые однозначные цифры неразличимы, тогда плоскость окажется покрытой одинаковыми Т-матрицами, между которыми стоят нули (относительно Т-матрицы левее 1, выше 3, ниже 7 и правее 9).

Как отметить число, не называя его словами? В наглядной арифметике предлагается показывать цифры десятков и цифры единиц как точки на числовой плоскости. Точка указывается каким-либо вектором или фишкой, устанавливаемой в нужном месте.
При решении примеров сложения, умножения и др. возникают переходы, которые рисуем стрелочками между исходными цифрами слагаемых или множителей к цифрам ответов арифметических действий. Полученные рисунки из стрелочек-указателей являются отличными подсказками в визуальном геометрическом счёте. Эти схемы с указателями можно видеть на цифровых вертушках - механических учебных пособиях, допускающих поворот вокруг центра Т-матрицы..
Цифровая плоскость интересна сама по себе. Так, склейка точек с одинаковыми единицами в номерах даёт объект, в топологии эквивалентный тору (бублику) с десятью точками на его поверхности. Координатные линии навинчиваются на трубку тора с разной скоростью 3:1.
Цифровую плоскость можно покрыть одинаковыми нечётными крестами и одинаковыми чётными крестами. Под нечётным крестом понимаем фигуру с центром в 5 и соседними нечётными числами. Чётный крест имеет в центре нуль, планки креста накрывают соседние чётные цифры.

Незакрытым на плоскости остаётся небольшой квадратик без цифр, закрашенный чёрным цветом.
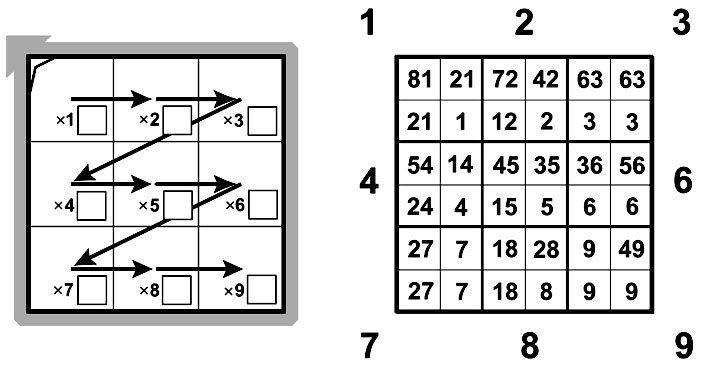
* Лист сложения представлен матрицей 3x3
|
Девятилистник сложения |
Структурное правило девятилистника сложения |
||
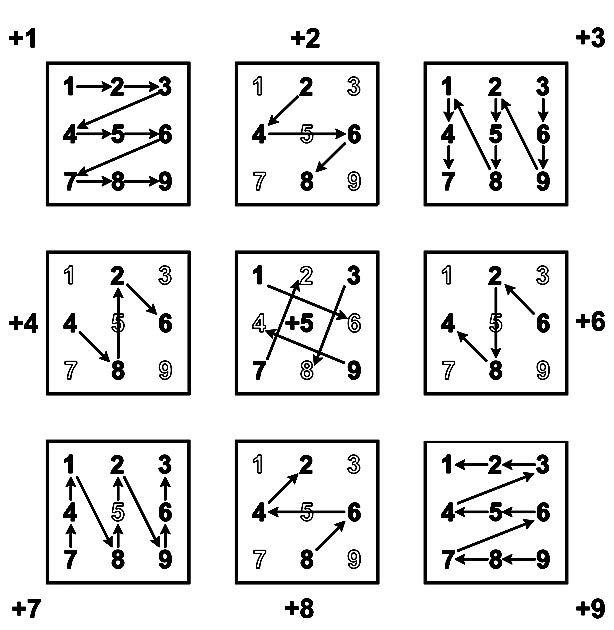 |
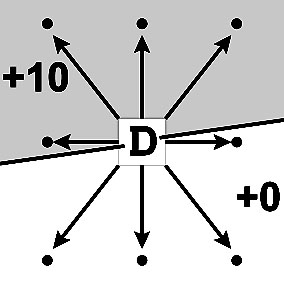
Примеры сложения однозначных чисел A + B = [ D; E ] показаны стрелочками - указателями A --> E. Десяток D = 1, если на указателе есть инверсия, то есть, A > E. На Т-матрице все направления можно показать как радиальные векторы, не имеющие инверсии (направлены направо или вниз), и векторы, имеющие инверсию (направлены налево или вверх). Разделяет два полупространства линия постоянного уровня (три шага направо и один шаг вверх).
|
Статья в файле PDF: Цифровые вертушки в игровом методе обучения сложению
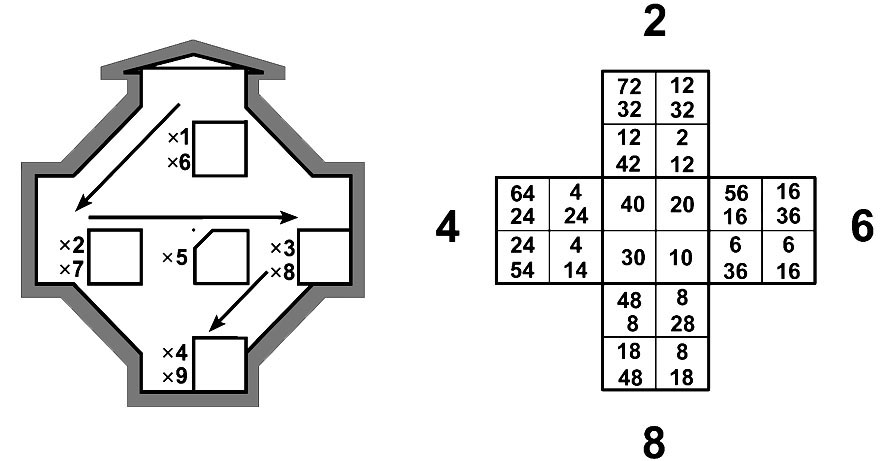
* Лист умножения представлен матрицей 3x3
Статья в файле PDF: Об идеальном формате таблицы умножения
Идея №2 эффективного счёта проистекает из особенностей позиционной десятичной системы счисления, учитывающей положение цифры в каком-либо разряде. Ясно, что 102 и 210 - это разные числа с одинаковыми цифрами в разрядах сотен, десятков, единиц.
Для некоторых примеров таблицы умножения однозначных чисел AxB=[D;E] с помощью простейших операций можно получить из множителей цифры произведения. Формулируются цифровые правила десятков D и цифровые правила единиц E.
По способу выражения можно отметить аналитические или геометрические правила.
Примеры: Правило умножения на десять Ax10=[D;E]=[A;0], приписать нуль справа от A.
Умножение на 9 даётся цифровой формулой, в которой разряды вычисляются аналитически Ax9 = [D;E] = [(A-1); (10-A)].
Можно рассматривать частные цифровые правила, действующие только на нескольких примерах (скажем, на чётных множителях).
В известной системе цифровых правил Трахтенберга, предложенных в середине XX века, делается попытка получить все ответы таблицы умножения Пифагора, применяя цифровые правила для всех примеров с фиксированным множителем A. Основная мысль состоит в том, что числовой результат можно получать, используя в качестве исходного материала величины A и B, их удвоенные значения 2xA, половинные A/2 и пятикратные значения 5xA. Однако часть применений правил Трахтенберга для младших множителей менее 5x5 оказывается сложнее самого процесса умножения. Нет у Трахтенберга простого правила умножения на 3.
Система цифровых правил наглядной арифметики существенно отличается от правил Трахтенберга. Покажем простое и эффективное правило умножения на 3 из арсенала наглядной арифметики, применив игровые методы обучения. Представим себе, что мы стоим в центре квадратной комнаты, превращенной в "цифровой класс". В углах и на стенах развесим листочки с цифрами, повторяющими формат телефонной панели. Цифра 5 будет у нас на полу под ногами.
Решаем пример 3xA=[D;E]. Повернемся лицом к цифре A. Покажем радиальный луч к исходному множителю A своей левой рукой.
Правило единиц для умножения на 3. Отведем правую руку в сторону под прямым углом к лучу нашего зрения на цифру A. Тогда правая рука укажет нам цифру единиц Е произведения 3xA.
Геометрическому правилу десятков для умножения на 3 можно придать следующий вид. Фишкой отметим полученную цифру единиц E на Т-матрице. В правом столбце Т-матрицы D=0, в среднем столбце десятки D=1, в левом столбце D=2. Мы "подсчитали" и указали цифры ответа произведения 3xA.
Почему применение геометрических алгоритмов можно называть счётом? Да потому, что мы получили правильные цифры ответа во всех случаях применения алгоритма. "Геометрический счёт" имеет свою "геометрическую логику", в которой последовательности геометрических действий эквивалентны арифметическому счёту и дают правильные цифры результатов.
В традиционной технологии счёта нет цифрового правила умножения на 3. В традиционных способах действий с числами не используется формат Т-матрицы, нет и поворота лучей Т-матрицы, необходимых для формулировки алгоритма. В наглядной арифметике доказано, что цифровое правило умножения на 3 невозможно сформулировать в линейных терминах, не привлекая цифровую плоскость.
Что же нужно добавить к допустимым операциям с числами, чтобы простой и очевидный геометрический поворот радиальных лучей на Т-матрице, помогающий мгновенно воспроизводить в визуальной памяти ответ умножения на 3, появился в стандартном учебнике арифметики? Этот вопрос в наглядной арифметике предлагается решать, внедрив специальные соглашения - стандарты, позволяющие двум людям разговаривать и мыслить в одной системе понятий.
Для успешного применения в устном счёте геометрических методов человек-вычислитель должен знать и применять стандарт Т-матрицы для устного счёта. Человек должен знать,
(1) где на телефонной матрице находится заданная цифра, и
(2) какая цифра находится в выбранной ячейке Т-матрицы.
Используя два геометрических правила стандарта Т-матрицы, строятся и другие схемы. Например, важно знать геометрические особенности линии, соединяющей числа в порядке возрастания. Эта линия называется "молнией" Т-матрицы. Особенностью формы ломаной линии "молнии" являются зигзаги, переходы из конца одной строки к началу другой нижней строки.
Важно! Нельзя допускать использования в устном счёте кем бы то ни было зеркального стандарта Т*-матрицы, так как правило умножения на 3 из правила правой руки станет вдруг "правилом левой руки". Если появятся сторонники стандартов, зеркальных к оппонентам, хаоса не избежать. Ученики одной школы будут учиться по одному стандарту, а другой школы - по другому. Как они будут разговаривать между собой и с экзаменаторами о математических законах числовых систем?
Заметим, кстати, что телефонная Т-матрица - это "правильная", "правосторонняя". Но клавиатура калькулятора и ки-пэд клавиатуры компьютера - "левосторонние", "неправильные" с точки зрения стандарта Т-матрицы, их нельзя применять для геометрического устного счёта, зеркальную Т*-матрицу нельзя упоминать в учебниках арифметики.
Применение геометрических цифровых правил вычислений базируется на положениях стандарта Т-матрицы для устного счёта. Вычислитель может мгновенно показать заданную цифру на Т-матрице и мгновенно понять, какая цифра находится в заданной ячейке Т-матрицы. Иначе говоря, простые алгоритмы указания "цифра"-"место" и "место"-"цифра" есть в арсенале действий человека-вычислителя. Теперь мы можем сосредоточить внимание на геометрических алгоритмах. Стандарт Т-матрицы гарантирует, что человек сможет выполнить эти геометрические алгоритмы на практике.
Вместо того чтобы называть каждое число и цифру словами, в визуальной технологии счёта указывается точка в фиксированной нумерованной конфигурации, например, на Т-матрице или цифровой плоскости.
Геометрические цифровые правила для единиц
Самым быстрым способом вычисления дополнения до полного десятка A*=10-A, (обозначаемое звездочкой), является указание симметричной точки для A относительно центра Т-матрицы. Например, пары (1 ←→ 9), (2 ←→ 8), (3 ←→ 7), (4 ←→ 6) на Т-матрице центрально симметричны, и в сумме дают 10.
Назовем пары множителей AxB и AxB* дополнительными. Пары множителей AxB и A*xB* называются симметричными.
Утверждение. Пусть A B - положительные целые числа.
Тогда единицы произведений для симметричных пар множителей равны
E ( A x B ) = E ( A* x B*).
Для доказательства рассмотрим разность
A* x B* - A x B = ( 10 - A ) x ( 10 - B ) - A x B = 100 - 10 ( A + B ).
Так как разность кратна 10, то единицы в записи симметричных множителей совпадают.
Итак, в таблице умножения Пифагора произведения, находящиеся симметрично относительно центра 5x5, имеют одинаковые цифры единиц.
Утверждение. Пусть E ( A x B ) ≠ 0.
Тогда единицы дополнительных пар множителей дополнительны друг к другу
E* ( A x B ) = E ( A x B* ).
Исключение составляют пары множителей, произведение которых кратно 10, то есть, цифра единиц E=0. (Дело в том, что дополнение нуля равно десятку 0*=10-0=10, а десяток не может быть цифрой в записи десятичного числа.)
Примеры. E(3x4) = E(12) = 2, Изменяем множитель на дополнительный E(3x4*) = E(3x6) = E(18) = 8, результаты дополнительны.
E(7x8) = E(56) = 6, Изменяем множитель на дополнительный E(7x8*) = E(7x2) = E(14) = 4, результаты дополнительны.
Для человека очевидны действия с малыми множителями. Зная результаты умножения с множителями менее 5, используя дополнение, мы мгновенно можем указать единицы для множителей более 5.
Например, E(1x1) = 1, поэтому E(1x1) = E(1*x1*) = E(9x9) = 1. В самом деле, 9x9=81.
E(2x2) = 4, поэтому E(2x2) = E(2*x2*) = E(8x8) = 4. В самом деле, 8x8=64.
Правила единиц для умножения, использующие поворот на Т-матрице
Обозначим буквой R геометрический поворот всех чисел Т-матрицы вокруг центра по часовой стрелке на прямой угол.
Тогда для нечётных чисел
|
R ( 1 ) = 3; ······ R ( 3 ) = 9; ······ R ( 9 ) = 7; ······ R ( 7 ) = 1. |
Центр 5 после поворота остается на месте, поэтому R ( 5 ) = 5.
Для чётных чисел
|
R ( 2 ) = 6; ······ R ( 6 ) = 8; ······ R ( 8 ) = 4; ······ R ( 4 ) = 2. |
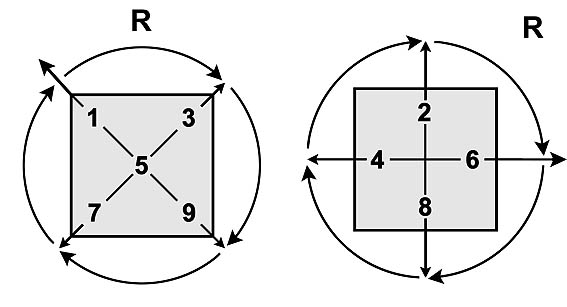
На Т-матрице нет нуля. Примем, по определению, что R ( 0 ) = 0.
Два последовательных поворота обозначим R R = R2.
Три последовательных поворота обозначим R R R = R3.
Очевидно, что четыре поворота R R R R = R4 приводят к тождественному отображению 1→1, 2→2 и т.д.
Верхний индекс при букве R означает число поворотов на прямые углы. Будем использовать отрицательные целые индексы (-1) для обозначения обратных поворотов всех чисел Т-матрицы на прямой угол против часовой стрелки.
Индекс числа поворотов при операторе R будем называть угловой мерой.
Угловая мера α ( A ) для однозначного нечётного числа A, не равного 5, может быть определена как число поворотов (на прямые углы) радиального луча числа 1 по часовой стрелке до совпадения с A
|
α ( 1 ) = 0: ······ α ( 3 ) = 1: ······ α ( 9 ) = 2: ······ α ( 7 ) = 3. |
Угловая мера для ненулевого однозначного чётного числа определена как число поворотов (на прямые углы) радиального луча числа 6 по часовой стрелке до совпадения с A
|
α ( 6 ) = 0: ······ α ( 8 ) = 1: ······ α ( 4 ) = 2: ······ α ( 2 ) = 3. |
Угловая мера чисел 5 и 0 не определена.
(Заметим, что математически можно ввести обобщённую угловую меру однозначных чисел, для которой α(5) и α(0) принимают значения, равные бесконечности ∞).
Изучим, как выглядят правила единиц умножения, если в арсенале вычислителя есть поворот R на прямой угол по часовой стрелке на Т-матрице.
Правило единиц умножения на 3.
Единицы произведения 3xA указаны повёрнутым лучом R(A).
Формула E ( 3 x A ) = R ( A ).
Правило единиц умножения на 9.
Единицы произведения 9xA указаны двумя поворотами луча R R (A) = R2 (A).
Формула E ( 9 x A ) = R 2 ( A ).
Утверждение. Два поворота луча на прямые углы эквивалентны отражению относительно центра поворота. Поэтому два поворота равны дополнению
R R (A) = R 2 ( A ) = 10 - A.
Правило единиц умножения на 7.
Единицы произведения 7xA указаны поворотом луча множителя A против часовой стрелки на прямой угол.
Формула E ( 7 x A ) = R -1 ( A ).
Правило единиц умножения на 5.
Единицы произведения 5xA равны 5, если A нечётно, и равны 0, если A чётно.
Для чётных множителей, которые будем обозначать буквой H,
геометрические правила единиц умножения будем показывать на чётном
кресте Т-матрицы. Пусть H число из множества {2, 4, 6, 8}.
Правило единиц умножения на 6.
Единицы произведения 6xH равны H
Формула E ( 6 x H ) = H .
Правило единиц умножения на 8.
Единицы произведения 8xH указаны повёрнутым лучом R(H).
Формула E ( 8 x H ) = R ( H ).
Правило единиц умножения на 4.
Единицы произведения 4xH указаны двумя поворотами луча R R (H) = R 2 (H).
Формула E ( 4 x H ) = R 2 ( H ).
Правило единиц умножения на 2.
Единицы произведения 2xH указаны поворотом луча множителя H против часовой стрелки на прямой угол.
Формула E ( 2 x H ) = R -1 ( H ).
Правило единиц умножения на 0.
Очевидно, что умножение на 0 даёт 0.
Формула E ( 0 x A ) = 0.
Преимуществом геометрических цифровых правил единиц для умножения, использующих поворот на Т-матрице, является их очевидность, возможность мгновенного выполнения в устном счёте.
на Т-матрице
Типичная конструкция цифровой вертушки состоит из двух плоскостей, на которых нарисованы Т-матрицы и, если необходимо, другие фигуры. Плоскости закреплены на оси в центре, и допускают поворот относительно друг друга.
Через центры матриц проходит ось вращения, перпендикулярная их плоскостям. Дальняя от нас плоскость неподвижна, она называется основной плоскостью или основой. На основной плоскости размещают числовые результаты умножения (или только единицы результатов). Можно сделать на поворачиваемой плоскости пропеллера цифровой вертушки вырезы или использовать прозрачную плоскость, сквозь которую видны числа на основной плоскости.
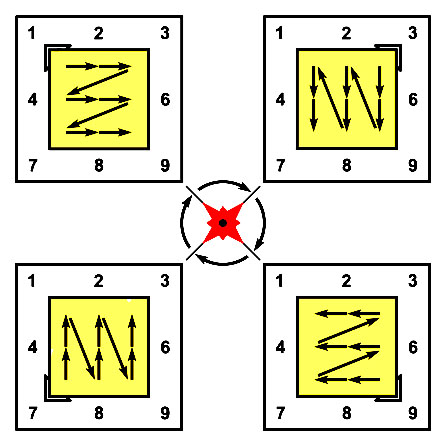
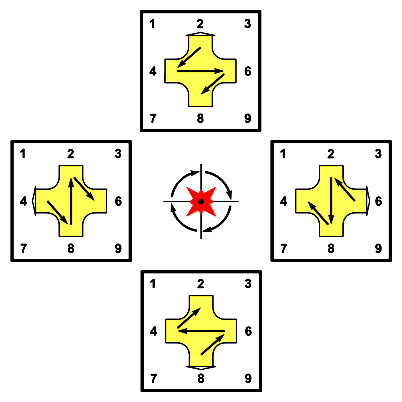
Для базовой конструкции вертушки потребуется два разных пропеллера цифровой вертушки (1) с рисунком нечетной молнии и (2) с рисунком чётной молнии. Узлы молнии пронумерованы по порядку появления на ломаной линии молнии 1-2-3-4…
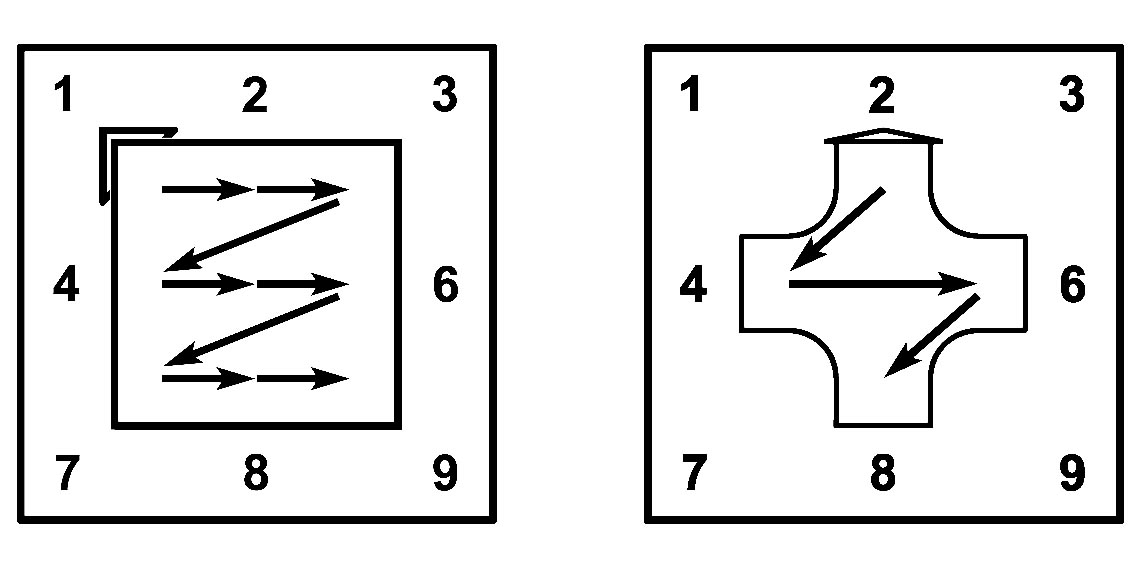
В исходном положении молний мы видим 1-й лист (нечётная молния) и 2-й лист (чётная молния) девятилистника. Четыре положения поворота пропеллера показывают разные листы умножения. Начальный узел молнии, нарисованный на пропеллере, указывает число A на основной Т-матрице. (Это – постоянный множитель A для всех примеров умножения на листе).
Ломаная линия из указателей A-молнии, изображённая на пропеллере, позволяет прочитать последовательные результаты умножения (Ax1); (Ax2); …; (Ax9).
Планетарная модель «вращения планет» на девятилистнике умножения
Сравнение линий молнии показывает, что на нечётных листах 1, 3, 7, 9 мы наблюдаем одну и ту же фигуру нечётной молнии в разных положениях поворота. Фигура молнии перемещается с одного листа на другой как твёрдое тело. Если задать траекторию перемещения между листами девятилистника в виде окружности, то нечётную молнию можно представлять как планету, облетающую центральное светило.
За время поворота по орбите вокруг центрального солнца «планета» – нечётная молния поворачивается вокруг своей оси на такой же угол. Любопытно, что планета всегда повернута к солнцу одной и той же стороной, как и Луна при вращении вокруг Земли. Числа на неподвижной Т-матрице листа умножения указывают постоянные направления на «далёкие звезды».
В таблице умножения на девятилистнике есть вторая «планета» – чётная молния, которая показана на чётных листах. Она поворачивается не только вокруг светила, но и вокруг своей оси.
В комбинациях и соотношениях чисел на двух поворачивающихся плоскостях цифровых вертушек можно увидеть и "прочитать" все ответы элементарных арифметических примеров сложения, вычитания, умножения и целочисленного деления.
Меняя рисунки на пропеллере вертушки и на основной неподвижной плоскости, получаем несколько любопытных вариантов, которые можно использовать в игровых методах обучения визуальной технологии счёта.
Вращающаяся таблица умножения представляет собой изделие из класса цифровых вертушек и показывает с помощью поворота "пропеллера" в специальных окошках шаблона результаты умножения на заданный множитель.
Для чётного множителя берём пропеллер вертушки с чётной молнией и соответствующий шаблон.
Математический смысл цифрового правила поворота не меняется в зависимости от того, какую цифровую вертушку мы используем. Однако существенно меняется терминология, с помощью которой излагаются геометрические алгоритмы указания цифр ответов. Различные терминологии геометрических правил наглядной арифметики рассматриваются как сходные игровые учебные ситуации, помогающие изучить алгоритмы визуальных вычислений.
Сравним способы реализации правила единиц для умножения 3xA=[D;E], применяя разные цифровые вертушки.
Вертушки "часы умножения". Представляют собой Т-матрицу с центральной осью, на которую надеты две радиальные стрелки короткая и длинная. Угол между стрелками можно менять, но при поворотах угол между стрелками остаётся неизменным. Короткая стрелка показывает исходный множитель. Величина угла между стрелками иллюстрирует правило умножения на разные множители, длинная стрелка показывает на цифру единиц результата умножения. Жестко скрепим две стрелки, надетые на центральную ось, так, чтобы от короткой (толстой) стрелки длинная (узкая) стрелка показывала бы направо под прямым углом (правило 3x...). Закрепим между двумя стрелками прямой угол.
Алгоритм указания единиц умножения на 3. Повернём уголок из двух стрелок (образующих прямой угол) до совпадения короткой стрелки с радиальным лучом луч множителя A. Тогда длинная стрелка покажет цифру единиц произведения 3xA=[D;E].
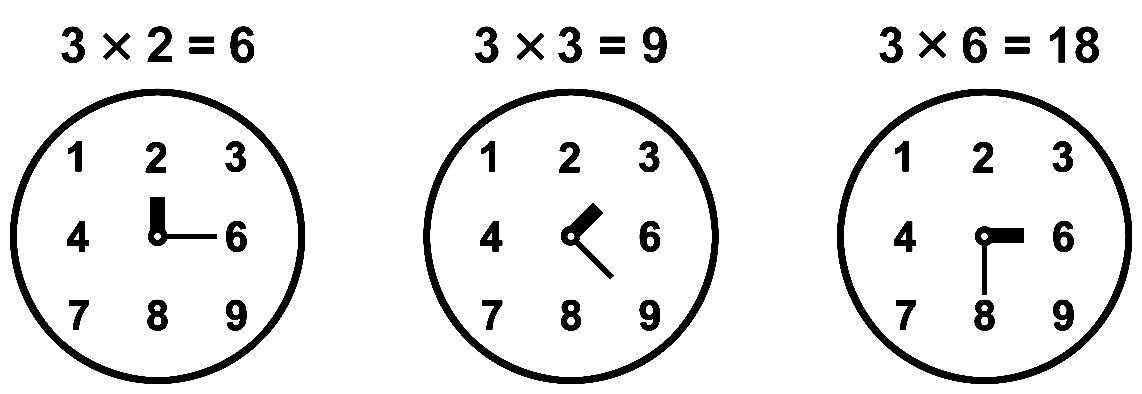
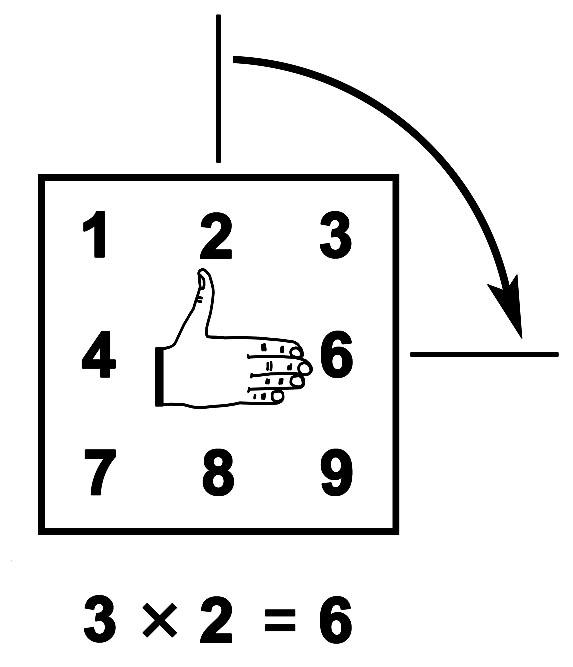
Вертушки "компьютер на пальцах". Большая Т-матрица нарисована на листе бумаги. Роль пропеллера вертушки выполняет ладонь, у которой большой палец составляет с плотно сжатыми остальными пальцами постоянный угол. На правой руке отставим в сторону большой палец. Положим ладонь правой руки на центр Т-матрицы, накрыв число 5.
Алгоритм указания единиц умножения на 3. Поворачивая ладонь вокруг центра, как на оси, совмещая направление большого пальца и радиальный луч множителя A. Если трудно повернуть руку на большой угол, поверните листок бумаги. Теперь сомкнутые пальцы правой руки показывают цифру единиц произведения E(3xA).
Для других множителей используем схему-справочник с разными уголками, показанными пальцами рук.
От пропеллера вертушки можно отказаться, если показывать направления своими руками, см. далее.
Допустим, ученик, знакомый с геометрическими цифровыми правилами наглядной арифметики разговаривает с учителем математики, причём придирчивым учителем. Ученик говорит, что умножил 3 на 2, используя правило "правой руки". Он, встал в центр Т-матрицы, повернулся лицом к множителю 2, затем справа от себя прочитал цифру единиц произведения 3x2=6. Иначе говоря, ученик правильно применил правило умножения на 3, записанное в книге по наглядной арифметике.
Вопрос учителя может озадачить: "Почему этот ответ правильный?" В математической школе иногда предлагают подобный тренинг: "Это действительно так, но я не верю, докажите".
Можем помочь ученику, предложив следующие аргументы. Нужно ответить, что "алгоритм проверен для всех случаев применения в таблице умножения. Во всех случаях получен правильный результат".
Если вы не воспользуетесь нашим советом, вам придётся строить доказательство правила умножения на 3, используя координатную запись поворота вектора на Т-матрице. Получите длинное и утомительное доказательство.
Доказательство правильности алгоритма вычисления опирается на некоторые теоремы, а те, в свою очередь, на аксиомы, принимаемые без доказательства.
Известны две системы аксиом натуральных чисел, которые предложили
(1) Дж. Пеано (1858-1932), (обобщение понятия числовой линии),
В аксиомах Пеано используется понятие "следующий элемент" (фактически, сложение +1).
(2) Г. Кантор (1845-1918), (теория множеств).
Подход Кантора использует взаимно однозначное соответствие элементов множеств. Классы равномощных конечных множеств отождествляются с натуральными числами. Подробнее этот вопрос освещал Бурбаки.
И в аксиомах Пеано, и в аксиомах Кантора среди арифметических действий первым появляется сложение, затем умножение.
* * *
Геометрические правила умножения, использующие повороты лучей на Т-матрице, можно рассматривать как формальную систему со своими аксиомами. Эту систему аксиом исследовал В.Б. Творогов (2011 г.) в монографии о наглядной арифметике и технологии быстрого счёта.
Формализованное описание арифметики, в котором сначала вводится умножение натуральных чисел, а, затем, сложение, будем называть непифагоровой арифметикой.
Для первоначального знакомства с системой аксиом непифагоровой арифметики предлагается использовать содержательную геометрическую интерпретацию, представляющую собой некоторую модель формальной системы. Геометрические преобразования можно показать на моделях механических цифровых вертушек, использующих повороты лучей на Т-матрице. Повороты пропеллера вертушки рассматриваются как ортогональные преобразования плоскости, оставляющие неподвижной фиксированную точку.
Проведём следующий эксперимент с числами. Обозначим некоторые цифры буквами E=1, R=3, H=6, V=5. Конечная последовательность букв означает умножение натуральных чисел. В ответах будем записывать только цифры в разряде единиц.
Два натуральных числа X, Y эквивалентны, если у них одинаковые цифры в разряде единиц X ~ Y. Например, 6 ~ 26. Пусть Q - любое натуральное число. Легко проверить, что справедливы следующие свойства умножения (необходимые условия)
|
(1) E Q ~ Q, (2) R R R R ~ E, (3) H H ~ H, (4) V V ~ V, (5) R V ~ V. |
1
x Q = Q 3 x 3 x 3 x 3 = 81 ~ 1 6 x 6 = 36 ~ 6 5 x 5 =25 ~ 5 3 x 5 = 15 ~ 5 |
Каждое правило имеет определённый смысл.
Эквивалентность (1) показывает, что символ E можно вычеркнуть, если есть другие символы.
Четыре символа R можно вычеркнуть, согласно (2), заменяя буквой E.
По правилу (3) символ H не дублируется.
Аналогично из (4) символ V не дублируется.
В соответствии с (5) можно сократить R, если в одночлене уже есть символ V, иначе говоря, "V поглощает R".
Рассмотрим правила (1) - (5), полагая, что символы являются операторами преобразования радиальных лучей для цифр нечётного креста {1, 3, 9, 7} с центром в точке 5, и, одновременно, преобразования радиальных лучей чётного креста {6, 8, 4, 2} с центральной точкой 0.
(1) Символ E - тождественное преобразование, не меняющее лучей.
(2) Четыре геометрических поворота R радиального луча на прямой угол приволят в исходное состояние.
(3) H - оператор переноса нечётных лучей на чётные лучи по правилу умножения на 6, то есть, H(A)-> E(6xA).
(4) Оператор H действует на лучи нечётного креста, стягивая их в центральную точку 5, и
H действует на лучи чётного креста, стягивая их в центральную точку 0.
(5) На плоскости поворот R оставляет на месте центральную точку нечётного креста.
Введём формальную систему S, называемую алгеброй цифровых вертушек, состоящую из всех конечных наборов символов {E; R; H; V},
S = { E, EE, ..., R, RR, RRR, ER, H, EH, ..., V, VH, ..., VHR, ... }.
Конечный набор символов из множества S называется одночленом (формальным словом). Формальное умножение двух одночленов Q1 и Q2 состоит в приписывании всех букв из Q2 к одночлену Q1. Формальное умножение, по определению, коммутативно: Q1 Q2 ~ Q2 Q1.
К некоторым одночленам можно применить правила сокращения, то есть, заменить некоторые комбинации букв по правилам (1) - (5). Правило сокращения, примененное к последовательности букв, по определению, не меняет значения одночлена.
Одночлен, к которому нельзя применить правило сокращения, называется неприводимым.
Справедлива теорема, которую сформулируем без доказательства.
Теорема 1. В формальной системе S с правилами (1) - (5) существует десять неприводимых одночленов:
E, R, RR, RRR, H, HR, HRR, HRRR, V, HV.
Теорема 2. Имеется два изоморфизма между умножением неприводимых одночленов алгебры вертушек и умножением однозначных чисел (с точностью до единиц). Эти изоморфизмы задаются соответствием
(1). E=1, R=3, H=6, V=5;
(2). E=1, R=7, H=6, V=5.
Показывая эти числа на Т-матрице, получаем для равенств (1) - основной изоморфизм, для равенств (2) - "зеркальный" изоморфизм.
Полагаем необходимым наметить идеи доказательства теоремы 2. Очевидно, E=1. Умножая все элементы из множества S на один и тот же символ, получим после применения правил сокращения некоторое количество элементов. При умножении на R≠1 получим 10 разных одночленов, это можно проверить вычислениями по правилам сокращения. Поэтому R - нечётно. Так как RR≠E=1, то R≠9. Легко проверить, что R≠5, иначе бы осталось после умножения RS только два элемента. Итак, остаются два допустимых варианта присваивания чисел R=3 или R=7.
Умножая элементы из S на H, получим 5 разных элементов (которыми могут быть только чётные числа), поэтому H - чётно. Одночлен VH соответствует нулю, поскольку поглощает все приписанные к нему символы.
Решая уравнение XX~X, получим варианты {0, 1, 5, 6}. Но 1 и 0 уже заняты, поэтому для V и H остаются числа 5 или 6. Так как H - чётно, то H=6. Множество SV имеет только 2 разных элемента {V, VH}, поэтому V=5. Теорема доказана.
Для того чтобы правило умножения на 3 было правилом "правой руки", мы будем использовать только основной изоморфизм, показывая числа на Т-матрице.
Итак, с помощью основного изоморфизма установлены соответствия чисел и неприводимых одночленов:
|
1 ~ E |
3 ~ R | 9 ~ RR | 7 ~ RRR |
| 6 ~ H | 8 ~ HR | 4 ~ HRR | 2 ~ HRRR |
| 5 ~ V | 0 ~ HV |
Результаты теорем 1 и 2 позволяют говорить о том, что аксиомами (1) - (5) введены десять однозначных чисел, для которых задана обычная операция умножения. Равенство чисел пока определено с точностью до единиц.
Следующий шаг в построении множества натуральных чисел заключается в том, чтобы определить:
во-первых, способ записи чисел по десятичным разрядам: единицы (уже есть), десятки, сотни и т.д.,
во-вторых, задать операцию сложения чисел, чтобы была выполнена аксиома дистрибутивности (A+1)B=AB+B.
Эта задача не представляет большой сложности, так как мы ежедневно применяем в счёте и десятичную систему записи чисел, и поразрядные действия с числами.
Таким образом, задача определения множества натуральных чисел посредством алгебры цифровых вертушек с аксиомами умножения (1) - (5) (и аксиомами дистрибутивности - для сложения) получает полное решение.
Изложенный здесь подход к определению множества натуральных чисел является новым способом аксиоматического введения натуральных чисел в математику, независимым от аксиом Пеано и аксиом Кантора. Вводя натуральные числа посредством аксиом непифагоровой арифметики, мы предполагаем существование геометрического пространства, в котором есть четыре стороны света (поэтому допустимы 4 поворота на прямые углы).
Подробнее см. статья: "Цифровые вертушки и непифагорова арифметика как способ определения натуральных чисел"
непифагоровой
арифметике
Введём функцию α(A), определённую для однозначных целых чисел A, принимающую целые значения, которую будем называть угловой мерой числа.
Угловая мера числа α(X) для нечетных чисел 1, 3, 7, 9 измеряется числом шагов поворота от начального радиального луча (5-->1) по часовой стрелке. Каждый шаг поворота равен прямому углу. После четырёх поворотов радиальный луч возвращается в исходное положение. Угловая мера α(X) для нечётных чисел X из множества { 1, 3, 7, 9 } принимает значения
|
α ( 1 ) = 0: ······ α ( 3 ) = 1: ······ α ( 9 ) = 2: ······ α ( 7 ) = 3. |
Угловая мера чисел 5 и 0 не определена.
Отсчёт угловой меры для чётных чисел выполняется на чётном кресте от начального вектора (5®6). Каждый шаг поворота равен прямому углу. Угловая мера α(H) чётных чисел H из множества {2, 4, 6, 8}
|
α ( 6 ) = 0: ······ α ( 8 ) = 1: ······ α ( 4 ) = 2: ······ α ( 2 ) = 3. |
Не определены величины угловых мер α (5) и α (0) для чисел 5 и 0, являющихся центральными числами. Для многозначного числа A угловая мера определяется по разряду единиц E (A): α (A) = α ( E(A) ).
Теорема 3. Пусть A – однозначное число, A ≠ 5 и A ≠ 0. Угловая мера α(A) равна показателю степени основания R = 3 в каноническом разложении числа A =̃ 3 α 6 N, где степени 0 ≤ α ≤ 3, 0 ≤ N ≤ 1.
Доказательство. Канонические разложения на множители по основаниям { 3, 6 } приведены в следующем списке
1 = 3 0, 3 = 3 1, 9 = 3 2, 7 =̃ 3 3;
6 = 3 0 x 6, 8 =̃ 3 1 x 6, 4 =̃ 3 2 x 6, 2 =̃ 3 3 x 6.
Из этих эквивалентностей следует утверждение теоремы. ■
Теорема 4. Пусть множители A и B не являются центральными числами 5 и 0.
Тогда угловая мера произведения равна сумме угловых мер множителей α ( A x B ) = α ( A ) + α ( B ).
В алгебре цифровых вертушек действуют три правила наследования свойств от множителя к произведению:
(1) наследование четности множителей (наличие у множителя символа H),
(2) наследование центральности множителей (наличие у множителя символа V),
(3) суммирование угловых мер множителей, если они определены.
Пример. 3 x 2 = X. Угловая мера α ( 3 ) = 1; α ( 2 ) = 3. Наследуются четность множителя 2 и сумма угловых мер множителей
α ( 3 ) + α ( 2 ) = 1 + 3 = 4. Число X должно быть чётно и иметь угловую меру α ( X ) = 4 (mod 4) = 0. Из теоремы 3 - это число X = 6.
Теорема 5. Чтобы вычислить цифру единиц E произведения однозначных чисел A x B, достаточно знать:
(1) чётность множителей A и B,
(2) центральность множителей A и B,
(3) сумму α (A) + α (B) угловых мер множителей, если они определены.
Конструкция цифровой вертушки идеально заимствует три правила наследования свойств множителей. Правила наследования чрезвычайно полезны для устного счёта. В самом деле, проверка чётности и центральности множителей выполняется мгновенно. Для вычисления цифры единиц E(AxB) достаточно сложить угловые меры множителей A и B, определяя угловую меру произведения.
Пример. 2 x 2 = ?
Используем эквивалентность 2~HRRR.
2 x 2 = HRRR HRRR = HH (RRRR) RR = H E RR = HRR ~ 4.
Применены правила сокращения HH=H, RRRR=E; EQ=Q.
В непифагоровой арифметике доказательство факта 2 x 2 = 4 выполняется иначе, чем в арифметике с аксиомами Пеано:
2 x 2 = (1+1) x 2 = 1 x 2 + 2 = 2 + 2 = (1+1) + (1+1) = (1+1) + 1 + 1 = (2 + 1) + 1 = 3 + 1 = 4.
Можно ввести обобщенную угловую меру числа, принимающую на числах 5 и 0 значение, равное бесконечности α(5) = α(0) = ∞. Сложение с бесконечностью даёт бесконечность α(A) + ∞ = ∞.
Пример. 3 x 5 = ?
По правилу наследования чётности X - нечётно. Угловая мера α ( 3 ) = 1; α ( 5 ) = ∞. Сумма α ( 3 ) + α ( 5 ) = 1 + ∞ = ∞. Нечётное число, у которого угловая мера равна бесконечности, - это число 5.
В непифагоровой арифметике можно вычислить только единицы произведения. Десятки в произведении множителей появляются после того, как к имеющейся операции умножения добавляется соглашение о разрядах десятичных чисел и определяется операция сложения.