Стандартная (пифагорова) арифметика основана на навыках счета с помощью загибания пальцев. Таблица умножения заучивается словами типа "дважды два - четыре". Это приводит к медленному проговариванию слов в процессе устного счета.

Наглядная арифметика изучает свойства геометрических конфигураций и связь с цифровыми правилами арифметики. Зная геометрическое цифровые правила, устный счет можно превратить в легкий, быстрый и приятный процесс умственной работы, почти мгновенно дающий числовые ответы.

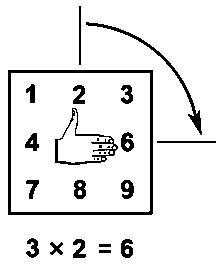
Правая рука показывает правило умножения на 3. Глядя из центра Т-матрицы, на множитель A, видим справа цифру единиц E произведения 3хA.

        Момент становления наглядной арифметики, как раздела математики, можно указать точно - 10.10.1999. В этот день был опубликован патент РФ с описанием изобретения - вращающейся таблицы умножения. Оказывается, взаимные повороты двух телефонных Т-матриц позволяют прочитать среди возникающих комбинаций цифр все ответы умножения однозначных чисел.

         Цифровые вертушки относятся к новому типу инструментов вычислений. Они не похожи по принципу действия на абак (счеты с камешками), костяные счеты или логарифмическую линейку.

         Во вращающейся таблице умножения применяется принцип поворота радиальных лучей, отличающий класс механических цифровых вертушек. Геометрические цифровые правила на Т-матрице подсказывают ответ любого арифметического действия. Умножение однозначных чисел заменяется одним поворотом луча, указывающим цифру единиц произведения.

         Устный счет с использованием геометрических цифровых правил выполняется мгновенно, со скоростью осознания визуальных образов.

   Сначала научитесь находить цифры на телефонной матрице, представляя себе, что находитесь в её центре.

   В наглядной арифметике цифры и числа не называют словами, а указывают на Т-матрице или на другой конфигурации.

   В идеале визуальный алгоритм - это непрерывная последовательность перемещения и изменения образов, как в кино.

   Для большинства алгоритмов имеются геометрические схемы, одновременно показывающие и исходные цифры и цифры результатов.

   Начинайте с простых примеров. Повторяйте алгоритмы многократно. Повышайте скорость работы до такого уровня, при котором невозможно произносить слова.

   Научитесь быстро складывать 3 однозначных числа в одной вычислительной операции. Увеличивайте число слагаемых до 4 или 5.

   Не стоит произносить слова для примеров умножения типа "пятью пять двадцать пять". Повторяйте шаги визуального алгоритма вычисления столь быстро, чтобы произнесение слов отстало по скорости. Вы увидите в памяти цифры результата быстрее, чем произнесете слова.

   Скорость выполнения операций должна быть такой, чтобы вы всё успевали.  Вычисления в уме - это сфера мышления. Скорость мышления растёт постепенно. У мышления есть свои концептуальные визуальные образы, своя логика. Скорость появления в визуальной памяти геометрического образа занимает малые мгновения. Поэтому визуальный счёт почти в 10 раз быстрее аудиомоторного счёта.

   Применяйте для обучения и самообучения цифровые вертушки. Используйте игровые методы для изучения правил наглядной арифметики. Рассказывайте учителю способ получения цифр решения. Замените словесные ответы учителю показом перемещений на Т-матрице.  

   Правила счета и алгоритмы изучайте по порядку. На практике применяйте выборочно то, что изучили.

   Для каждого примера нужно запомнить геометрический алгоритм решения, а не только общие цифровые правила. Цифровые правила, записанные формулами, нужно использовать в теории, доказывая утверждения. В практике счёта запоминаемые буквенные выражения и математические обозначения формул замедляют вычисления. Вместо формул лучше использовать визуальные схемы "компьютера на пальцах", цифровые вертушки и др. геометрические образы.

   Рекорды скорости придут сами, когда будут освоены все элементарные действия.

     Учёт возрастных особенностей детей очевиден, нужна простая терминологии, игровые методы обучения, минимум формул. Доказательства утверждений наглядной арифметики доступны школьникам, изучающим алгебру.

Теория наглядной арифметики основана на системе аксиом непифагоровой арифметики, в которой умножение однозначных чисел определяется раньше, чем сложение. 

     Автор - Творогов Владимир Борисович - математик. Родился в 1951 году, живет в Москве. Окончил с отличием механико-математический факультет Московского государственного университета. Кандидат физико-математических наук.

     Однажды, занимаясь с сыном Алёшей скучным повторением таблицы умножения, случайно заметил закономерность поворота цифр на телефонной матрице. Глубокое математическое исследование этого удивительного факта заняло длительное время. Результатом стали многочисленные статьи и патенты, посвященные классу цифровых вертушек, а также - книга о наглядной арифметике и быстром счете.

       Все права защищены.  Допускается некоммерческое использование материалов этого сайта в учебных целях.

       Описание наглядной арифметики использует следующие патенты РФ, принадлежащие автору:

       Творогов В. Б. Вращающаяся таблица умножения. Патент РФ № 2139574. 10.10.1999.

       Творогов В. Б. Способ обучения и модель таблицы умножения на основе девяти матриц – девятилистника. Патент РФ № 2139575. 10.10.1999.

       Творогов В. Б. Динамическая модель таблицы умножения, использующая указатели цифр, понятные инопланетянам. Патент РФ № 2174713. 10.10.2001.

       Творогов В. Б. Цифровые вертушки для сложения, вычитания, умножения и целочисленного деления, использующие телефонную Т-матрицу. Патент РФ № 2406160. 10.12.2010. Бюл. № 34.

       Творогов В. Б. Цифровые вертушки для вычисления квадратов двузначных чисел, использующие телефонную Т-матрицу. Патент РФ № 2432617. 20.10.2011. Бюл.№ 30.

        Мы приводим на сайте математические утверждения, существенные для правильного понимания технологии быстрого устного счета. Математические утверждения не относятся к объектам промышленной собственности, но имеют авторство.

         Коммерческое использование материалов книги или патентов возможно только на основе письменных договоров с правообладателями.

         Просьба при цитировании указывать ссылки на источники.