Основные понятия
наглядной арифметики
Геометрические
пространства
Геометрическое пространство - это линия, плоскость или пространство.
Выделенные точки - фиксированные точки пространства, которым приписаны натуральные (или целые) числа.
Числовая линия (или числовая ось) - линия, на которой выделен ряд точек на равном расстоянии. Выбранной точке приписано число нуль 0. Правила расстановки других чисел "шаг направо - это плюс 1". Будем называть традиционной или пифагоровой арифметикой систему представлений, в которой для изображения арифметических действий используется числовая линия и не используется числовая плоскость.

Цифровая линия - это числовая линия, на которой у всех чисел стерты разряды десятков, сотен и старше. Остаются только разряды единиц в десятичной записи чисел.
Числовая плоскость - плоскость с декартовой (прямоугольной) системой координат. Натуральные числа приписаны точкам с целочисленными координатами по правилу строки: "шаг направо - это плюс 1", и правилу столбца: "шаг вниз - это плюс 3".
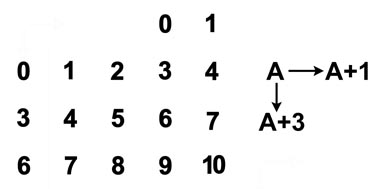
Цифровая плоскость - это числовая плоскость, на которой у всех чисел стерты разряды десятков, сотен и старше.
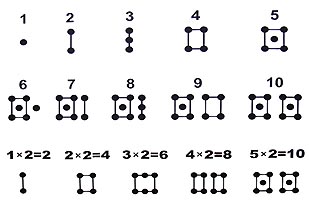
Все одинаковые однозначные числа считаются неразличимыми между собой (склейка точек).

| Конфигурации "по 2" с центральной точкой. Конфигурации "по 3". Выделение пятерок | ||
 |
 |
|
Т-матрица

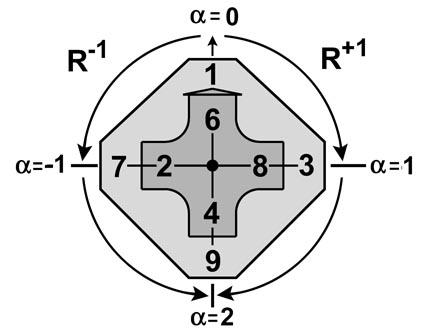
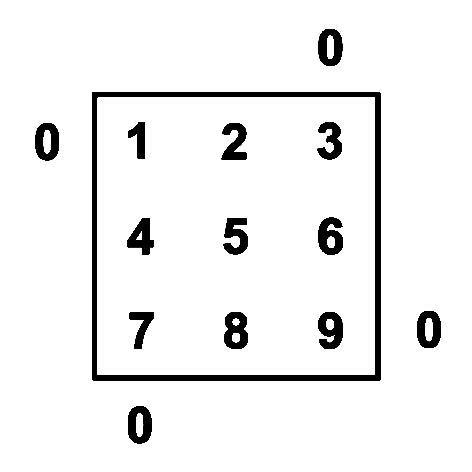
Т-матрица - матрица из трех строк и трех столбцов. Левый верхний угол занимает число 1.
Правила расстановки других чисел задают правило строки "Шаг направо - это плюс 1" и правило столбца "Шаг вниз - это плюс 3" от текущего значения числа..
Т-матрица является частью числовой плоскости и частью цифровой плоскости.
В наглядной арифметике цифровые правила используют геометрические признаки расположения чисел на Т-матрице.
|
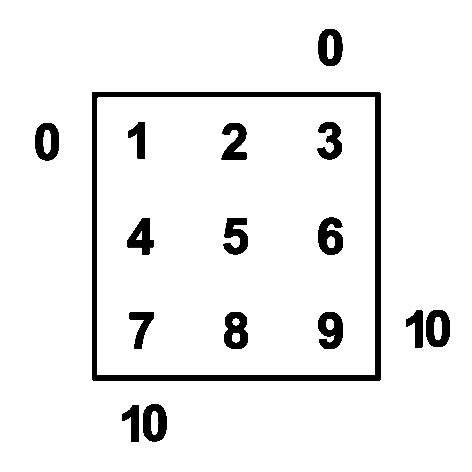
На Т-матрице нет нуля 0, поэтому приходится рассматривать Т-матрицу на числовой плоскости, рядом с которой расположены нули 0 и числа 10. Расширенная Т0 - матрица - это часть цифровой плоскости, содержащая Т-матрицу и расположенные рядом нули 0.
|
 |
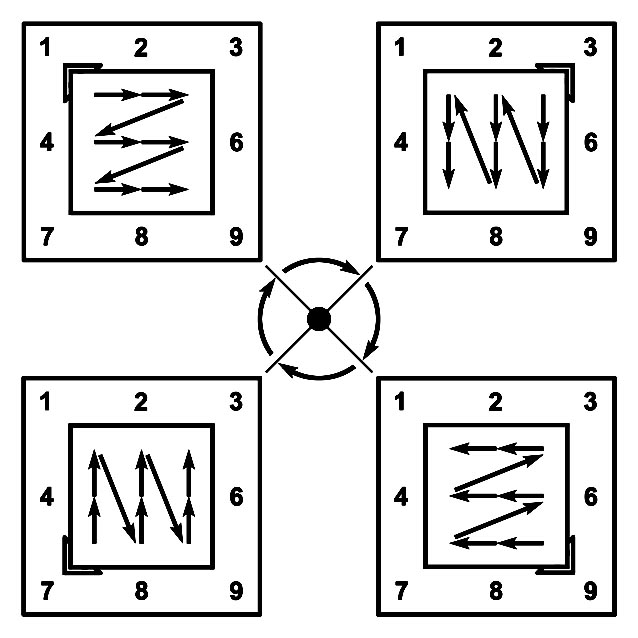
Молния Т-матрицы
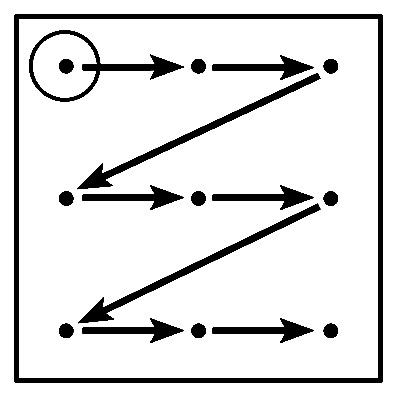
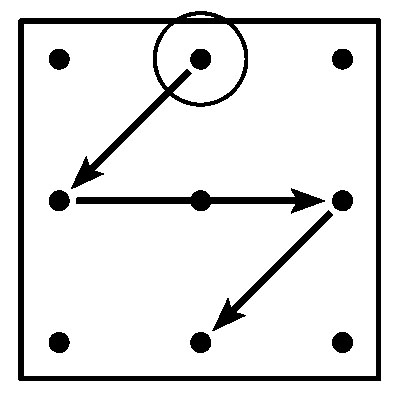
| Нечетная молния Т-матрицы | Четная молния Т-матрицы |
 |
 |
Линия, проходящая по числам Т-матрицы в порядке возрастания, называется нечетной молнией.
Линия, проходящая по четным числам Т-матрицы в порядке возрастания, называется четной молнией.
Молния Т-матрицы состоит из векторов-указателей.
Точки, которым приписаны числа на молнии называются узлами. Узлы нумеруются в порядке появления на линии молнии.
Первый узел молнии называется начальным узлом.
Стандарт Т-матрицы
для устного счета
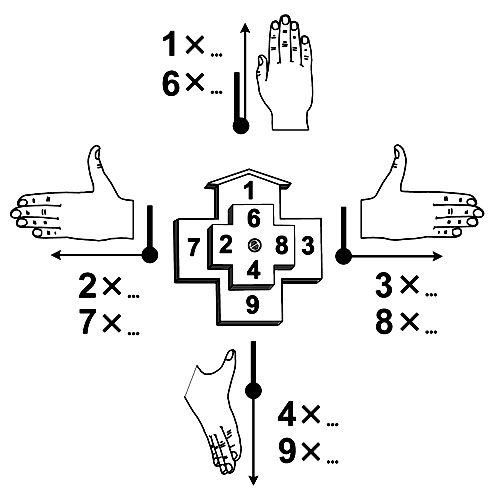
Геометрические методы вычислений в наглядной арифметике используют телефонную Т-матрицу.
В требованиях стандарта Т-матрицы для устного счета предполагается, что человек, изучающий визуальную технологию быстрого счёта, должен уметь решать две взаимосвязанные задачи.
1) По заданному однозначному числу A нужно быстро определять место расположения числа A на Т-матрице.
2) По заданной ячейке Т-матрицы нужно быстро определять число A, находящееся в этой ячейке.
Например, для числа 3 эти требования стандарта Т-матрицы означают, что правый верхний угол Т-матрицы и число 3 для человека-вычислителя ассоциируются как тождественные визуальные образы. Требования стандарта Т-матрицы очевидны, но должны выполняться человеком мгновенно, что достигается тренировкой.
Иной формат мы увидим, поставив зеркало сбоку от рисунка. Принятый в наглядной арифметике, де факто, стандарт Т-матрицы, имеет своего зеркального дублера - Т*-матрицу. В зеркале изображения похожи, но правое и левое поменялись местами. Поэтому правило правой руки умножения на 3 превращается в зеркальном аналоге в правило левой руки.
Применяемый стандарт правостороннего или левостороннего изображения числовой плоскости в технологии устного счета должен быть один, и только один. Дело в том, что цифровое правило применяется мгновенно, со скоростью реакции человека. Выполнять скоростную вычислительную работу приходится на уровне чувства. Некогда размышлять о том, что умножение на 3 может быть задано не правой, а левой рукой в зеркальном алгоритме для указания ответа. Основное и зеркальное изображения Т-матрицы в одной концепции устного счета совершенно несовместимы.
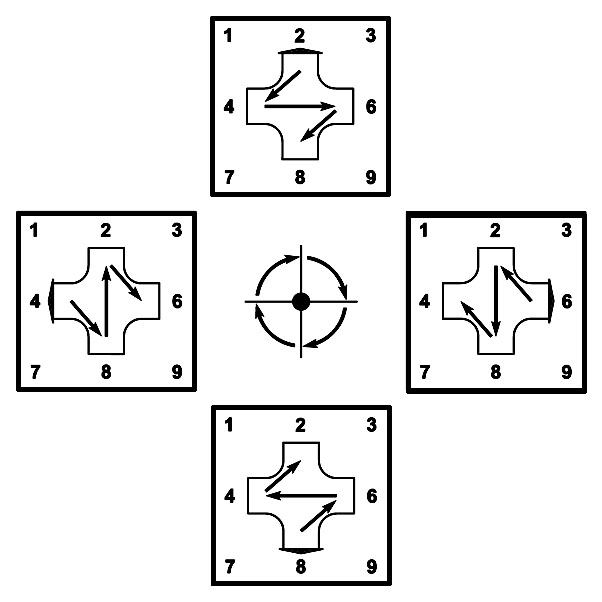
Цифровая вертушка
на Т-матрице
|
Цифровая вертушка с нечетной молнией
|
Цифровая вертушка с четной молнией
|
Цифровая вертушка имеет две плоскости, которые могут поворачиваться вокруг центральной оси.
Неподвижная плоскость называется основой.
Поворачивающаяся плоскость цифровой вертушки называется пропеллером.
Четыре положения поворота молнии на Т-матрице показывают планетарную модель вращения.
Центр планетарной системы занимает "солнце", этой центральной точке приписан пример "5´5=25".
|
|
|
|
Поворот пропеллера на прямой угол переводит радиальные лучи нечетных цифр в нечетные цифры, а радиальные лучи четных цифр - в четные цифры.
Начальный луч для нечетных чисел (5 --> 1) показывает на Т-матрице от центра к числу 1.
Начальный луч для четных чисел (5 --> 6) показывает на Т-матрице от центра к числу 6.
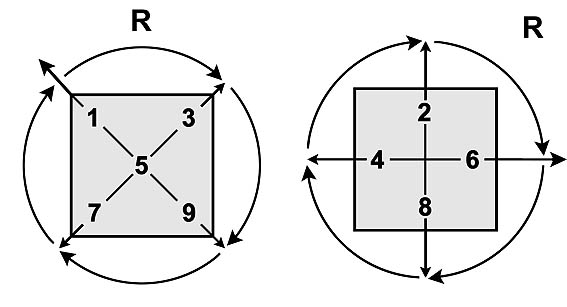
Поворот измеряется угловой мерой.
Поворот луча на прямой угол по часовой стрелке имеет угловую меру, равную 1.
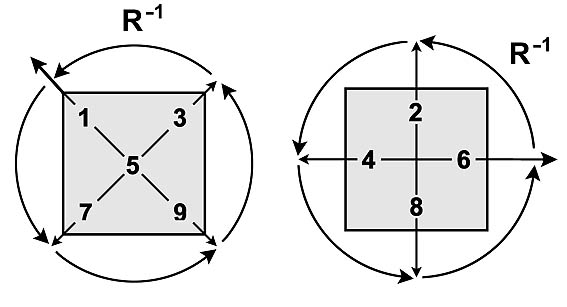
Поворот радиального луча против часовой стрелки будем обозначать отрицательной величиной угловой меры.
Поворот луча на прямой угол против часовой стрелки имеет угловую меру, равную (-1) (минус один).
Поворот луча на 4 прямых угла оставляет радиальный луч на месте, поэтому угловая мера определена с точностью до 4.
Компьютер "на пальцах"
Правило единиц
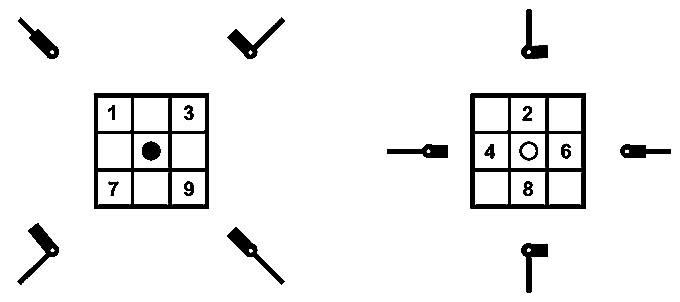
| "Галактические" уголки для вычисления единиц E(AxB) | Рука - инструмент вычисления | |
 |
|