Сложение

Сложение

с помощью конфигураций меток

        Натуральное число можно представить суммой единиц в его аддитивном составе A = 1+1+1+...+1.

        Сумма A+B определяется количеством единиц в составе обоих слагаемых. Для быстрого подсчета суммы меток можно использовать упорядоченные конфигурации слагаемых A и B. Конфигурации требуют перемещения нескольких меток, поэтому являются медленным способом подсчета.

        Самый быстрый метод подсчета элементов в множестве использует упорядоченные конфигурации, такие, как Т-матрица, и векторы-указатели ответов. Познакомимся с этим геометрическим методом указания цифр ответов более подробно.  

Сложение

с помощью указателей

Указатель ответа для примера сложения  A + B = [ D, E ].

          Вектор A --> E называется указателем единиц суммы (для сложения "+B").

          Вектор B --> E является другим указателем единиц суммы (для сложения "+A").

Допустим, что на плоскости выделено десять точек, которым приписаны однозначные натуральные числа 0, 1, 2, ..., 9.

Теорема. Каждому примеру сложения однозначных чисел соответствует вектор-указатель между выделенными точками.

Теорема. Каждому вектору-указателю между выделенными точками соответствует один конкретный пример сложения однозначных чисел.

       Геометрический алгоритм вычисления суммы A+B выполняется в три этапа:

       1) указываем исходную цифру A арифметического примера,

       2) вспоминаем положение вектора-указателя ответа (+B), выходящего из точки A,

       3) показываем с помощью указателя цифру единиц суммы E. 

       Стрелка указателя является подсказкой, показывающей цифру ответа. Указатели ответов позволяют человеку "решать" арифметический пример, вспоминая и считывая в уме цифры с визуального образа.

      Геометрические решения примеров сложения мы будем строить в каком-либо геометрическом пространстве:

на числовой линии, на числовой плоскости, на цифровой плоскости или Т-матрице.

      Числовая линия и числовая плоскость являются линейными пространствами.

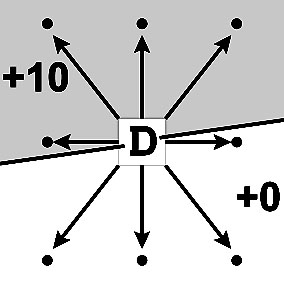
     Очевидно, что   A + 0 = [ 0, A ]. Этому примеру соответствует указатель 0 --> A, действие (+0) ничего не меняет.

     Вектор 0 --> A, начинающийся в нуле, будем называть указателем числа A.

     Параллельный перенос указателя числа "+B" в любую точку C стрелочкой показывает правильный ответ примера C + B.

     По правилу вычисления суммы точка E находится на конце указателя, величина D равна 1, если на указателе C --> E есть инверсия.

     Пример.  4 + 2 = ?  Начало указателя  0 --> 2 параллельным сдвигом переносим в точку 4. Теперь стрелочка показывает два шага направо от точки 4, здесь находится число 6. Инверсии нет. Поэтому D=0 и 4+2=6.

Примеры A + B = [ D; E ]

показаны стрелочками - указателями

A -->  E.

Десяток D = 1, если на указателе есть инверсия, то есть, A > E.

Инверсия

Статья в файле PDF: Цифровые вертушки в игровом методе обучения сложению

Девятилистник сложения

со всеми указателями

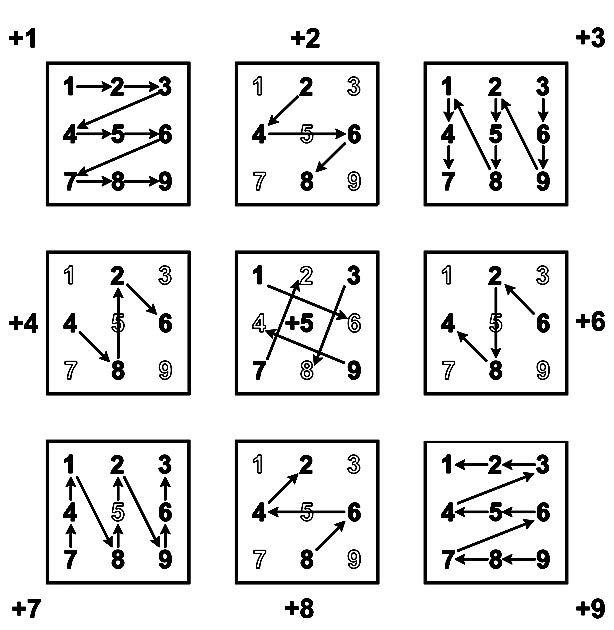
    Лист сложения - это множество примеров (A + B), у которых имеется одинаковое слагаемое "B". Нарисуем указатели единиц ответов для примеров каждого листа сложения на отдельных Т-матрицах.

Расположим рисунки девяти листов сложения в формате Т-матрицы.

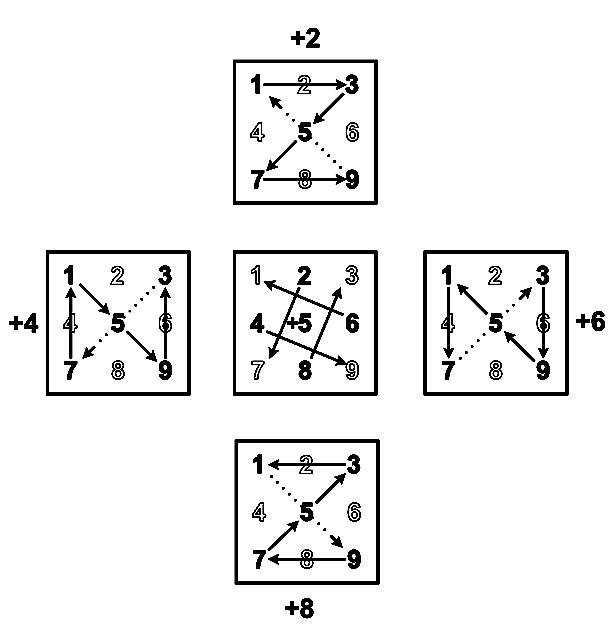
Получим фигуру, которую будем называть девятилистником сложения. На рисунке девятилистника представлены указатели примеров сложения однозначных положительных чисел. Чтобы не загромождать четные листы, указатели примеров сложения "нечет + чет" вынесены на отдельный рисунок.

Свойства молнии

Молния на каждом листе сложения начинается с числа Т-матрицы, которое называется номером этой молнии.

Молнии с номерами 1, 3, 9 и 7 похожи и являются поворотами одной и той же нечетной молнии Т-матрицы.

Молнии с четными номерами 2, 6, 8 и 4 также имеют общие признаки. Они являются поворотами одной и той же четной молнии.

Правила единиц

для сложения

Двузначные числа ответов будем обозначать двумя цифрами десятков и единиц, заключенными в квадратных скобках,  

       [ D, E ] = 10 D + E.

Решаем пример A + B = [ D, E ] с помощью молнии Т-матрицы.

      Правило единиц для сложения на Т-матрице.

1). Устанавливаем фишку на ячейку A на Т-матрице.

2). Вспоминаем положение B-молнии на Т-матрице. Определяем направление указателя (A --> E) на B-молнии, выходящего из точки A.

3). Перемещаем фишку по указателю молнии, выходящему из точки A. На конце стрелочки указателя читаем цифру единиц E суммы (A+B).

       Положение B-молнии на Т-матрице подсказывает цифровая вертушка. Берем молнию пропеллера цифровой вертушки той же четности, что и слагаемое B. Для нечетного слагаемого B применяем нечетную цифровую вертушку. Для четного слагаемого B используем четную цифровую вертушку.

Правила десятков

для сложения

На главную страницу