Общие свойства
| На главную страницу |
Лист умножения
Множители A x 1, A x 2, A x 3, ..., A x 9 образуют лист умножения с номером A.
Указатель единиц
для сложения
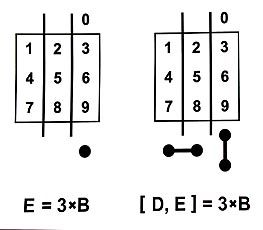
Запишем пример сложения A + B = [ D, E ].
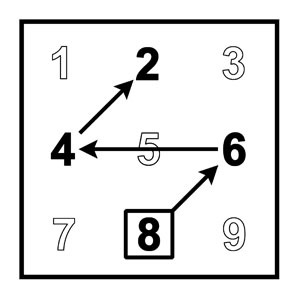
Пусть A - фиксировано. Можно показывать числа как точки в какой-либо конфигурации с нумерованными метками. Нам потребуется Т-матрица.
Вектор B --> E является указателем единиц сложения.
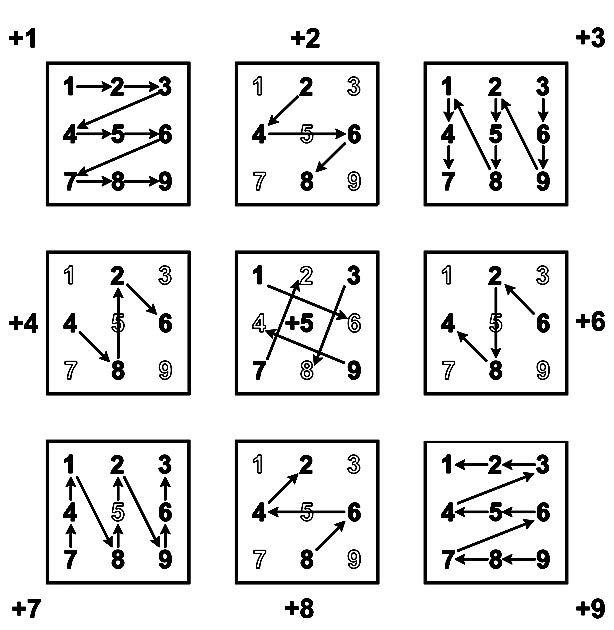
На Т-матрице указатели сложения (A+...) образуют A-молнию.
Девятилистник умножения
Напишем примеры умножения A x B = [ D, E ] на карточках.
Разложим карточки на девяти Т-матрицах, называемых листами умножения A=1, 2, ..., 9.
Поместим карточку примера A x B = [ D, E ] на листе A в ячейке с номером E, заданной цифрой единиц произведения.
Девятилистник умножения - это фигура, состоящая из девяти листов умножения, расположенных в формате, подсказанном Т-матрицей.
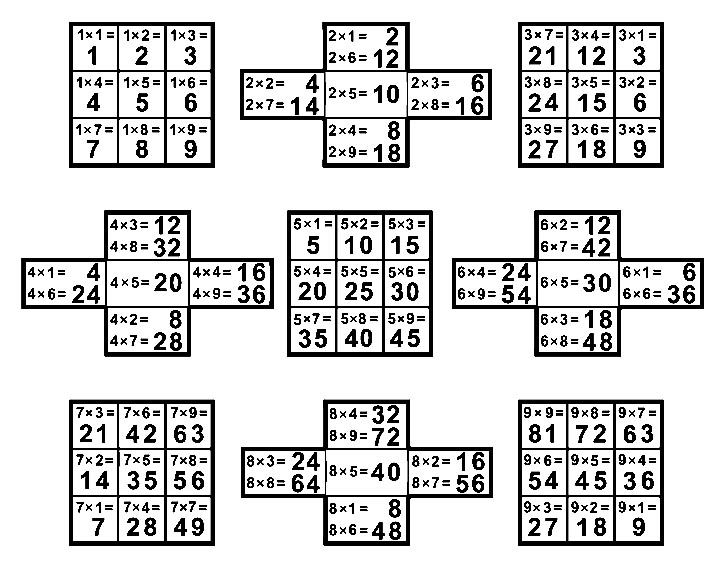 |
Порядок чтения примеров умножения Ax1, Ax2, Ax3, ..., Ax9 на A-листе задает A-молния Т-матрицы.
Четный лист умножения можно изобразить на двух Т-матрицах, оставив место посередине для результата умножения на 5.
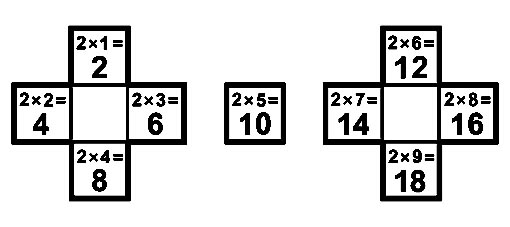
Вращающаяся таблица умножения
| Шаблон и основа нечётных листов | Шаблон и основа чётных листов |
 |
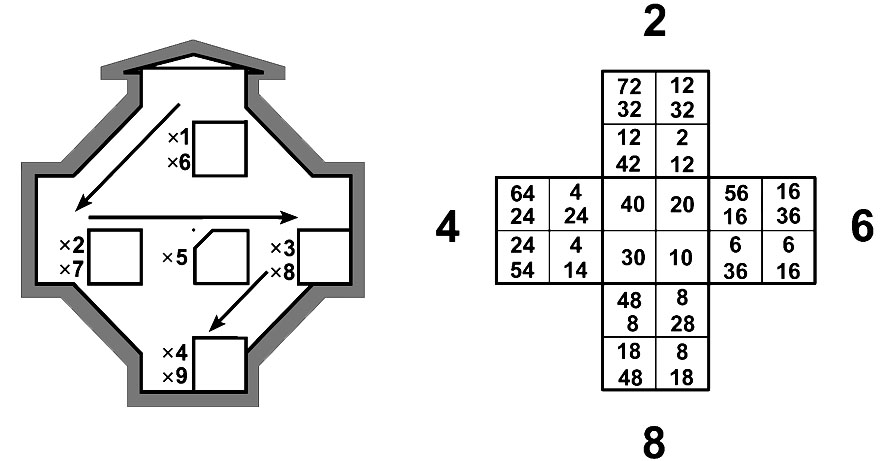 |
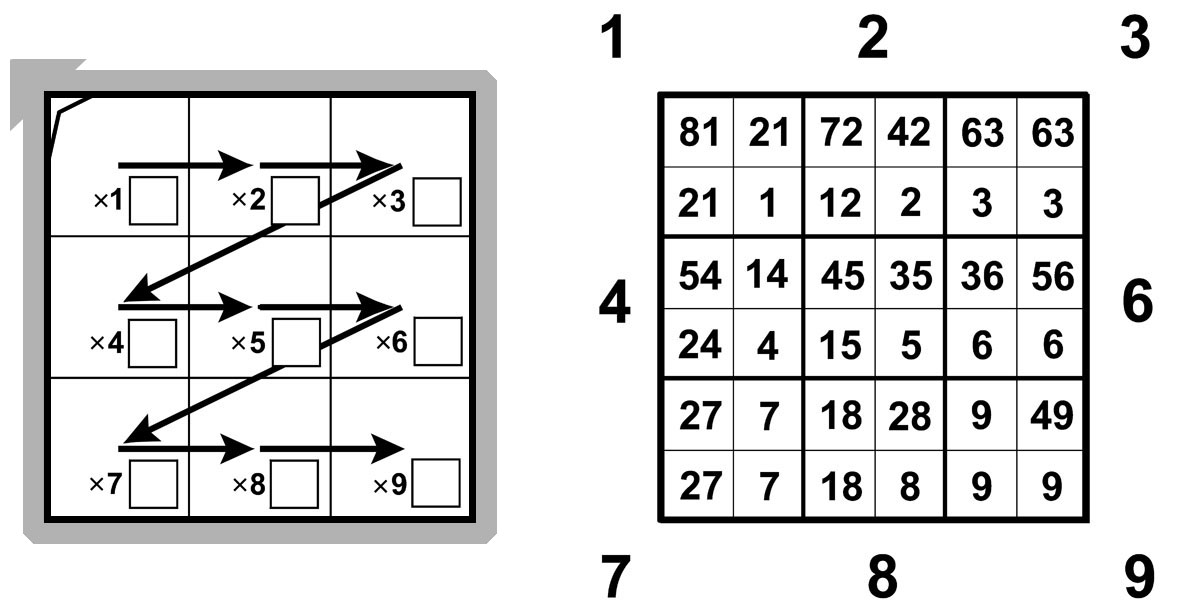
Вращающаяся таблица умножения показывает отдельные листы таблицы умножения при поворотах пропеллера.
На поворачивающейся плоскости сделаны вырезы, через которые видны цифры на основной плоскости.
Линию чтения примеров на листах с номерами 1, 3, 7, 9 задает нечетная молния.
Линию чтения примеров на листах с номерами 2, 4, 6, 8 обеспечивает четная молния.
Алгоритм вращающейся таблицы умножения.
(1) Выбираем шаблон по чётности множителя A.
(2) Поворачиваем пропеллер вертушки главным углом к множителю A.
(3) Находим на пропеллере узел молнии с номером B. Здесь читаем в окошке произведение AxB=[D;E].
|
Правила указания ответов |
(1)
Цифровые правила подстановки:
10xA = [A;
0],
(2) Аналитические правила по разрядам:
9xA = [(A –
1); (10 – A)],
5xA = [(A/2);
0], где [1/2; 0] = 10 / 2 = 5,
6xA = [(A/2);
A].
(3) Геометрические правила на Т-матрице.
Правила умножения
для единиц и десятков
на вращающейся таблице умножения
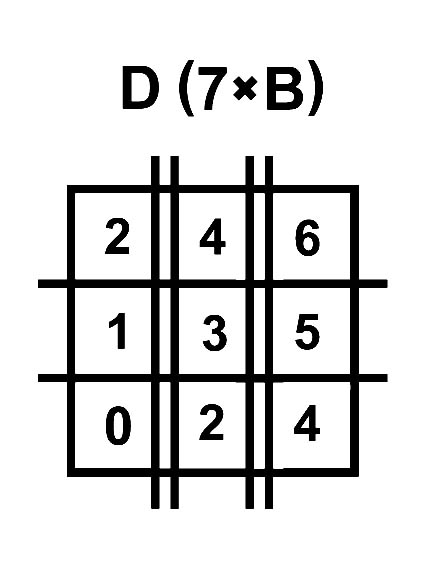
Цифра единиц E примера A x B = [ D, E ] находится на Т-матрице напротив узла B на A-молнии.
Цифра десятков D примера A x B = [ D, E ] равна числу инверсий на A-молнии от её начала до узла с номером B.
Общие правила будем изучать на примерах каждого конкретного листа умножения.
|
3-я молния |
Метод тени для делимости на 3 | |||
|
3-й лист |
Ступенчатая модель |
Границы десятков на Т |
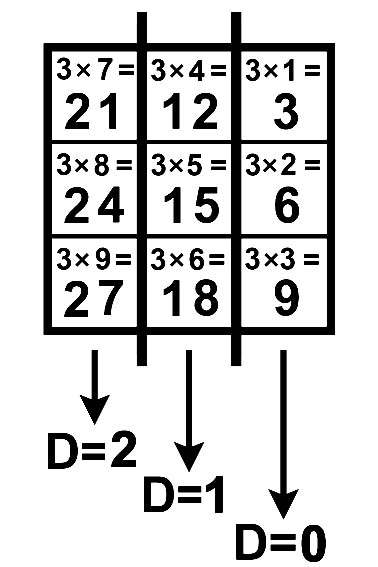
Делимость на 3 числа DE |
Делимость на 3 числа HDE |
 |
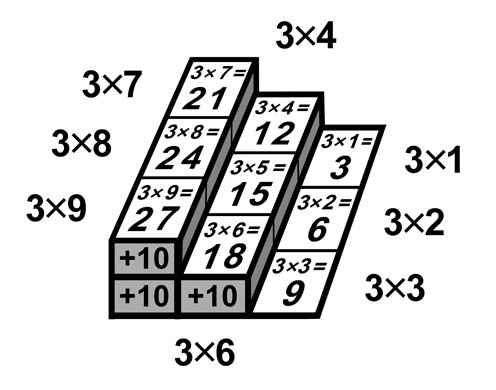 |
 |
 |
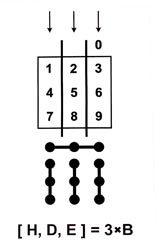 |
7-й лист умножения
|
7-й лист умножения |
"Компьютер на пальцах" 7xA |
||||
|
|
Ступенчатая модель |
Границы десятков на Т |
Правило единиц | Правило десятков | |
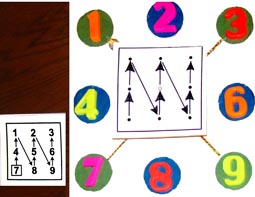 |
|
|
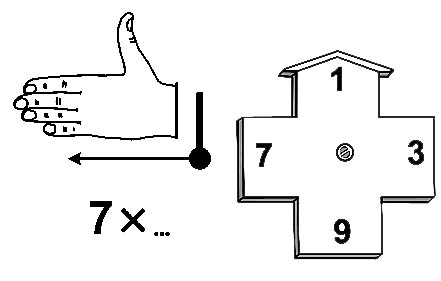 |
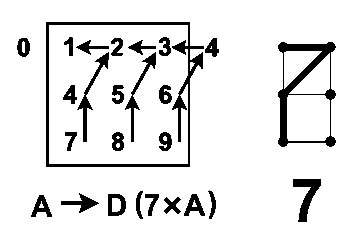 |
|
9-й лист умножения
| 9-я молния и цифровые правила 9xA | Признак делимости на 9 | ||
|
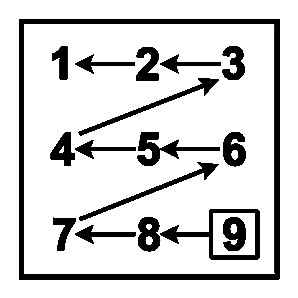
9-я молния |
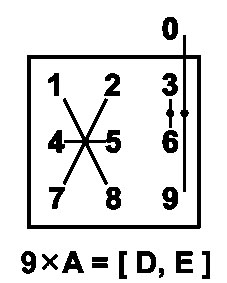
Цифровые правила |
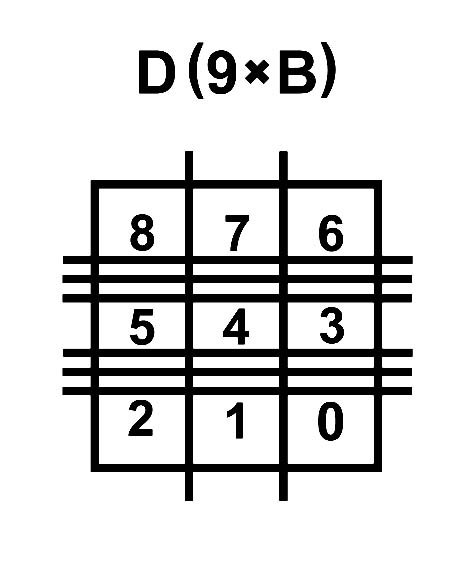
Границы десятков на Т |
Соединим точки D и E произведения 9xA на Т-матрице. Схема "жук ползет по стенке" - все числа до 99, кратные 9 |
 |
9xA = [(A - 1), (A*)] A* = 10 - A
|
 |
 |
|
2-я молния и ступенчатая модель |
Границы десятков на Т |
||
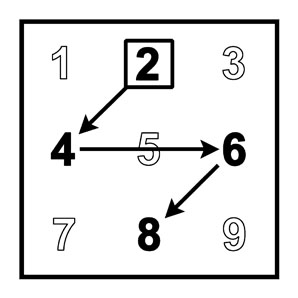 |
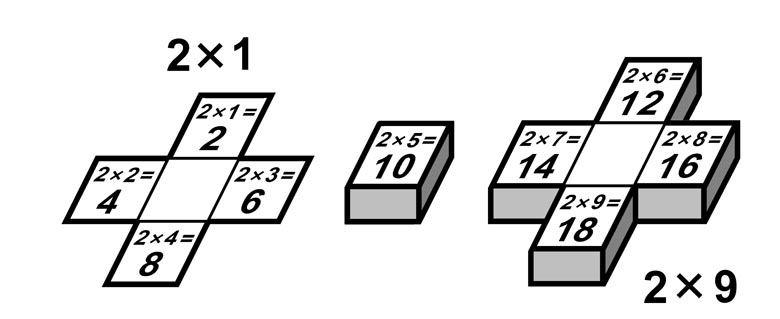 (A < 5) D = 0. (A >= 5) D = 1. |
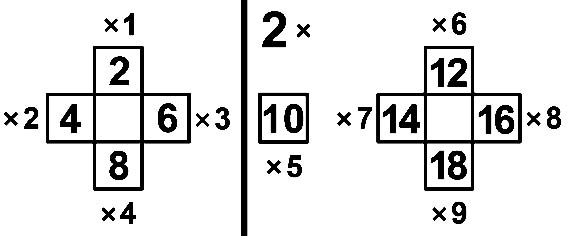 |
|
|
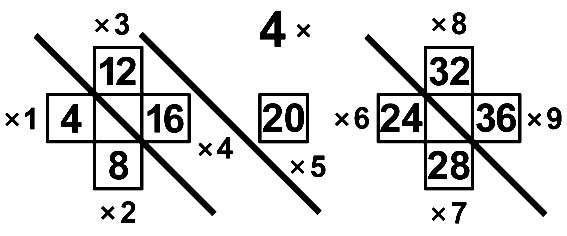
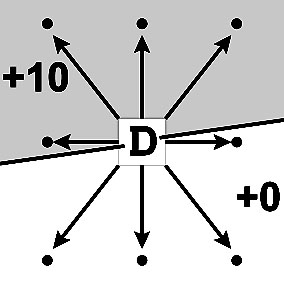
4-й лист умножения и ступенчатая модель 4xA Умножение 4xA (A=2,4,6,8) Умножение 4xA (A=1,3,7,9) |
Границы десятков на Т наклонные |
Инверсия |
||
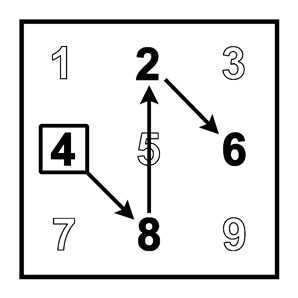 |
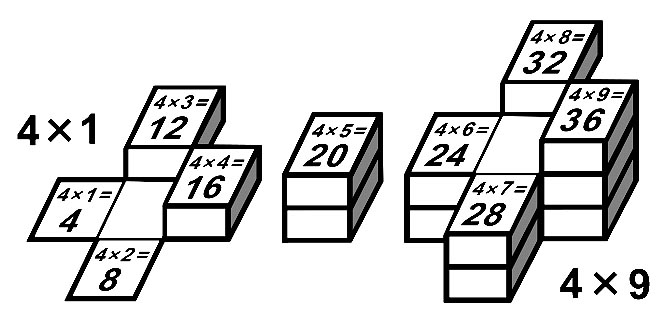 |
 |
 |
|
|
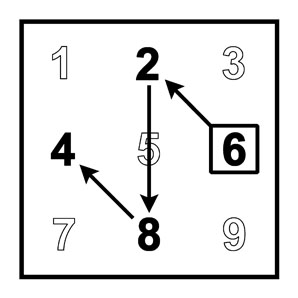
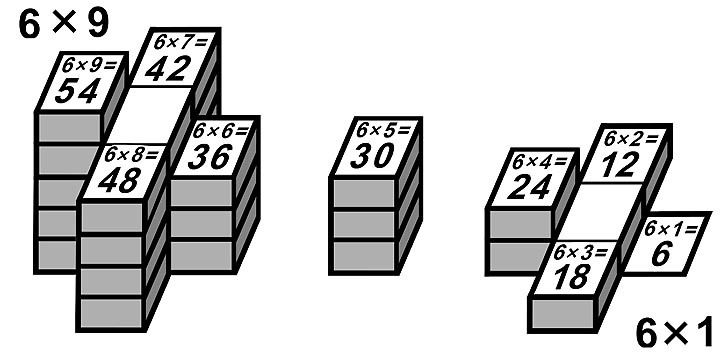
6-я молния и ступенчатая модель 6xA |
Границы десятков на Т вертикальные |
Инверсия |
||
 |
 |
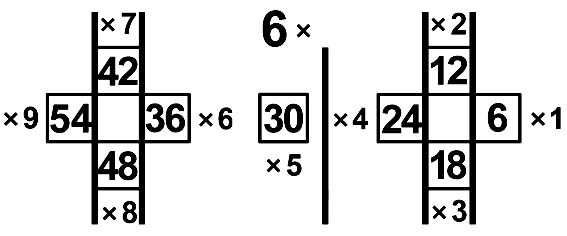 |
 |
|
|
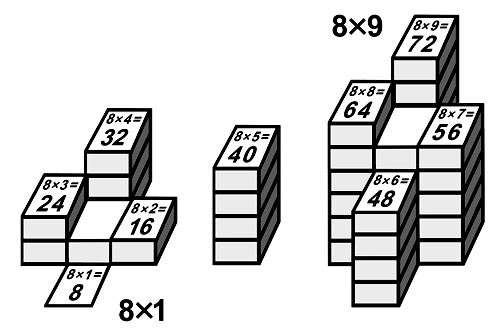
8-я молния и ступенчатая модель 8xA |
Правило десятков 8xA |
Границы десятков на Т |
|
|
|
|
A={ 1, 2, 3, 4, 5 } D=A-1. A={ 6, 7, 8, 9 } D=A-2. |
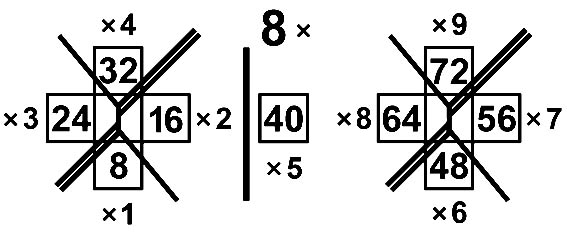 |