| На главную страницу |
| Статья для энциклопедии "Таблица умножения Пифагора" (автор В.Б. Творогов, 2013) |
Таблица умножения, она же таблица Пифагора — таблица, имеющая 10 строк и 10 столбцов, построенная в соответствии со следующим структурным правилом: строки и столбцы пронумерованы множителями A и B, ячейки таблицы содержат их произведения AxB.
В таблице умножения Пифагора применяется десятичная запись натуральных чисел.
Расширенная таблица умножения Пифагора представляет собой продолжение таблицы 10 x 10 для множителей более 10.
Используется для обучения школьников умножению. Первое известное в истории математики
изображение таблицы умножения в виде квадрата 10x10
приведено в книге «Введение в арифметику» Никомаха Геразского (I-II
век). Автор отмечал, что такое изображение таблицы умножения применял
Пифагор (ок. 570-500 г. до. н.э.). Цифры таблицы Пифагора были записаны
в ионийской нумерации, использующей 24 буквы греческого алфавита и 3
архаические буквы финикийцев (6=вау, 90=коппа, 900=сампи). Чтобы
отличить цифры от букв, над числами рисовали горизонтальную черту –
титло.
Первое известное в истории математики
изображение таблицы умножения в виде квадрата 10x10
приведено в книге «Введение в арифметику» Никомаха Геразского (I-II
век). Автор отмечал, что такое изображение таблицы умножения применял
Пифагор (ок. 570-500 г. до. н.э.). Цифры таблицы Пифагора были записаны
в ионийской нумерации, использующей 24 буквы греческого алфавита и 3
архаические буквы финикийцев (6=вау, 90=коппа, 900=сампи). Чтобы
отличить цифры от букв, над числами рисовали горизонтальную черту –
титло.
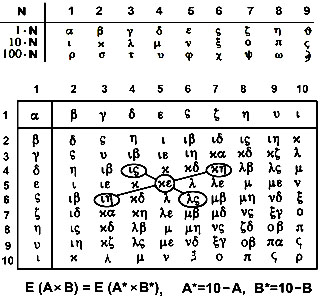 |
В таблице умножения Пифагора показана симметрия единиц
для множителей, расположенных симметрично относительно центра (5;5). Дополнение до полного десятка обозначено A*=10 - A. |
Имеются существенные отличия древнегреческой записи десятичных чисел от современной записи чисел по разрядам:
* не используется нуль,
* цифры-буквы 1, 2, …, 9 не используются для обозначения полных десятков, полных сотен и полных тысяч, которые обозначены собственными буквами.
Заметим, что у древних народов не было знаков суммы и разности. Если в паре чисел-букв левое число больше, то они суммируются, если левое число меньше, из правого числа-буквы вычитается левое. (Обратите внимание на запись римских чисел IX=9, X=10, XI=11).
В средние века в России и Европе часто применялось умножение AxB способом удвоения, не использующее таблицу Пифагора. Этот трудоёмкий алгоритм соответствует разложению второго множителя в некоторую сумму из степеней двойки: 1; 2; 4; 8; 16; 32; 64; 128; … Так, 6=4+2; 21=16+4+1. Производится умножение AxB(i).Все выделенные промежуточные результаты суммируются AxB = AxB(1) + … + AxB(n).
Владимир Даль
Солдатские досуги.
(1861)
Владимир Даль. Солдатские досуги. (1861)
Таблица умножения.
|
Волга Дону пошире: Дважды два четыре. |
У кого аршин, тому и мерять: Трижды три девять. |
Четырежды четыре шестнадцать, Четырежды пять двадцать. |
Кинь указку, пойдём гулять: Пятью пять, двадцать пять. |
|
Нет книг у дяди, а карты есть: Дважды три шесть |
Слушай ухом: без восьми двадцать: Трижды четыре двенадцать. |
На мосту - по-татарски - на купире: Четырежды шесть двадцать четыре. |
Коли нет, так нечего взять: Пятью семь – тридцать пять. |
|
Хлеб жнём, а сено косим: Дважды четыре восемь. |
Трижды пять пятнадцать, Трижды шесть осьмнадцать. |
Угодно откушать, так милости просим: Четырежды семь двадцать восемь. |
И мал золотник, да дорог: Пятью восемь сорок. |
|
Без закваски хлеб не месят: Дважды пять десять. |
Мучицы и маслица, вот тебе блин: Трижды семь двадцать один. |
Кто атаман, у того и булава: Четырежды восемь – тридцать два. |
Бери оглоблю, пойдём воевать: Пятью девять сорок пять. |
|
На руках, на ногах пальцев двадцать: Дважды шесть двенадцать. |
Мало ль диковин в Божьем мире: Трижды восемь двадцать четыре. |
Велика честь, да нечего есть: Четырежды девять тридцать шесть. |
Отлежал бока, от того и болят: Пятью десять пятьдесят. |
|
Пять пальцев долой - пятнадцать: Дважды семь четырнадцать. |
Днём свет, а ночью темь: Трижды девять двадцать семь. |
И крот в своём углу зорок: Четырежды десять сорок. |
|
|
Дважды девять осьмнадцать, Дважды десять двадцать. |
|
|
|
|
Мастер Самсоныч лапти плесть: Шестью шесть тридцать шесть. |
Дурни плодятся, не надо их сеять: Семью семь сорок девять. |
Не буянь у хозяина на квартире: Восемью восемь шестьдесят четыре. |
Делам своим всяк сам господин: Девятью девять восемьдесят один. |
|
Что заслужили, то и носим: Шестью восемь сорок восемь. |
Ино прилечь, ино присесть: Семью восемь пятьдесят шесть |
Живи, поколе на плечах голова: Восемью девять семьдесят два. |
Что хитро, то и просто: Девятью десять девяносто. |
|
Кто сказку слышал о царе Кире? Шестью девять пятьдесят четыре. |
Чего не знаешь, того не ври: Семью девять шестьдесят три. |
|
Полно долбить, покинь долото: Десятью десять сто. |
|
Полезай на стену, коли велят: Шестью десять шестьдесят. |
Рядком сумы на простенке висят: Семью десять семьдесят. |
|
|
Квадраты чисел
(2011)
Владимир Творогов (2011). Квадраты чисел.
| 1 × 1 = 1 |
Один на один – сам себе господин. |
| 2 × 2 = 4 |
Дважды два – четыре, это всем известно в целом мире. |
| 3 × 3 = 9 |
Три на три – у телефона девять цифр и много звона. |
| 4 × 4 = 16 |
Четыре собаки купались в реке, шестнадцать следов на песке. |
| 5 × 5 = 25 |
Пятью пять – двадцать пять, это надо знать! |
| 6 × 6 = 36 |
Шестью шесть – полна корзина, и десятков – половина |
| 7 × 7 = 49 |
Семью семь – сорок девять, не забудь проверить! |
| 8 × 8 = 64 |
Восемь на восемь – в шахматном мире клеток на поле шестьдесят четыре. |
| 9 × 9 = 81 |
Единицу от девятки отнеси направо, вот и вся забава! |
Для детей полезны стихи, активизирующие образную память. В стихах можно найти и яркие запоминающиеся образы, и некоторые цифровые правила получения чисел результатов.
Другие авторы могут добавить свои стихотворения на тему таблицы умножения.
и окрестности
базовых чисел
|
Расширенная таблица умножения Пифагора в десятичной системе |
||||||||||||||||||||
|
× |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
2 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
30 |
32 |
34 |
36 |
38 |
40 |
|
3 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
30 |
33 |
36 |
39 |
42 |
45 |
48 |
51 |
54 |
57 |
60 |
|
4 |
4 |
8 |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
40 |
44 |
48 |
52 |
56 |
60 |
64 |
68 |
72 |
76 |
80 |
|
5 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
100 |
|
6 |
6 |
12 |
18 |
24 |
30 |
36 |
42 |
48 |
54 |
60 |
66 |
72 |
78 |
84 |
90 |
96 |
102 |
108 |
114 |
120 |
|
7 |
7 |
14 |
21 |
28 |
35 |
42 |
49 |
56 |
63 |
70 |
77 |
84 |
91 |
98 |
105 |
112 |
119 |
126 |
133 |
140 |
|
8 |
8 |
16 |
24 |
32 |
40 |
48 |
56 |
64 |
72 |
80 |
88 |
96 |
104 |
112 |
120 |
128 |
136 |
144 |
152 |
160 |
|
9 |
9 |
18 |
27 |
36 |
45 |
54 |
63 |
72 |
81 |
90 |
99 |
108 |
117 |
126 |
135 |
144 |
153 |
162 |
171 |
180 |
|
10 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
120 |
130 |
140 |
150 |
160 |
170 |
180 |
190 |
200 |
|
11 |
11 |
22 |
33 |
44 |
55 |
66 |
77 |
88 |
99 |
110 |
121 |
132 |
143 |
154 |
165 |
176 |
187 |
198 |
209 |
220 |
|
12 |
12 |
24 |
36 |
48 |
60 |
72 |
84 |
96 |
108 |
120 |
132 |
144 |
156 |
168 |
180 |
192 |
204 |
216 |
228 |
240 |
|
13 |
13 |
26 |
39 |
52 |
65 |
78 |
91 |
104 |
117 |
130 |
143 |
156 |
169 |
182 |
195 |
208 |
221 |
234 |
247 |
260 |
|
14 |
14 |
28 |
42 |
56 |
70 |
84 |
98 |
112 |
126 |
140 |
154 |
168 |
182 |
196 |
210 |
224 |
238 |
252 |
266 |
280 |
|
15 |
15 |
30 |
45 |
60 |
75 |
90 |
105 |
120 |
135 |
150 |
165 |
180 |
195 |
210 |
225 |
240 |
255 |
270 |
285 |
300 |
|
16 |
16 |
32 |
48 |
64 |
80 |
96 |
112 |
128 |
144 |
160 |
176 |
192 |
208 |
224 |
240 |
256 |
272 |
288 |
304 |
320 |
|
17 |
17 |
34 |
51 |
68 |
85 |
102 |
119 |
136 |
153 |
170 |
187 |
204 |
221 |
238 |
255 |
272 |
289 |
306 |
323 |
340 |
|
18 |
18 |
36 |
54 |
72 |
90 |
108 |
126 |
144 |
162 |
180 |
198 |
216 |
234 |
252 |
270 |
288 |
306 |
324 |
342 |
360 |
|
19 |
19 |
38 |
57 |
76 |
95 |
114 |
133 |
152 |
171 |
190 |
209 |
228 |
247 |
266 |
285 |
304 |
323 |
342 |
361 |
380 |
|
20 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
220 |
240 |
260 |
280 |
300 |
320 |
340 |
360 |
380 |
400 |
произведение A×B ?
Примеры умножения на фиксированный множитель («лист умножения») в таблице Пифагора расположены вдоль линии. Линейный формат таблицы Пифагора не даёт универсальных подсказок о величине десятичных цифр D и E числового результата A´B.
В процессе устного счёта человек имеет несколько возможностей получить результат умножения чисел:
- запомнить результат как аудио фразу или визуальный образ памяти, затем, при необходимости, вспомнить результат данного примера,
- выполнить расчёт по формулам сокращённого умножения,
- воспользоваться определением умножения и просуммировать несколько чисел (начиная с некоторого базового значения).
- для многозначных чисел применить общую формулу поразрядного умножения (если упростить решение не удаётся),
Не все варианты действий приемлемы для эффективного счёта. Отбор эффективного способа решения осуществляется по нескольким критериям
- минимального времени выполнения умножения,
- минимума трудозатрат при вычислениях.
Линейные цифровые правила сокращённых вычислений
По определению, произведение A x B = [D; E] равно сумме B раз числа A:
A x B = A + A + …+ A.
Эффективное цифровое правило – это алгоритм, позволяющий указать цифры десятков D и единиц E произведения проще и быстрее, чем выполняется многократное сложение.
Если алгоритм выполняется по времени дольше, чем звучит заученная фраза типа «пятью пять – двадцать пять», то цифровое правило не эффективно.
Стандартные формулы сокращённого умножения, использующие дополнение.
Умножение на 10. Самое полезное цифровое правило – это правило умножения на 10: чтобы получить произведение, нужно «приписать нуль справа» Ax10=[A;0].
Умножение на 9. Сокращенное цифровое правило умножения на 9: десятки D=A–1 . единицы E=10–A.
Обозначим дополнение до полного десятка звездочкой: A*=10–A.
Из определения следует, что A + A* = 10. Например, 9+1=10, 8+2=10, 7+3=10, 6+4=10, 5+5=10.
Вычислительная формула 9xA= [ (A – 1); (10 – A)] = [ (A – 1); A*].
Умножение на 8.
Вычислительная формула 8xA = [ (A – 2); 8* x (10–A) ] = [ (A – 2); (2xA*) ].
Умножение на 7.
Вычислительная формула 7xA = [ (A – 3); 7* x (10–A) ] = [ (A – 3); (3xA*) ].
Умножение на 6.
(1) Вычислительная формула 6xA = [ (A – 4); 6* x (10–A) ] = [ (A – 4); (4xA*) ].
(2) Пусть H - чётное число. Тогда 6xH= [ (H/2); H ].
Пусть A -нечётное число. Тогда 6xA= [ {A/2}; (A + 5) ]. Здесь обозначено: {A/2} - целая часть числа A/2, дробная часть отбрасывается.
Умножение на 5.
5xA = [ (A/2); 0 ]. Здесь, по определению, [1/2; 0] = 5.
Для умножения в диапазоне от 1x1 до 5x5 стандартных цифровых правил нет, так как вычисление с помощью дополнения оказывается сложнее самого примера.
Обобщение. Правила сокращённого умножения с использованием дополнения.
Пусть A и B находятся в диапазоне {6, 7, 8, 9}. Произведение множителей выражается через дополнения
AxB = [ (A + B – 10); (A*xB*) ] = [ (A – B*); (A*xB*) ].
Упрощается умножение величин более 5, так как в разряде единиц остаётся произведение величин менее 5.
Недостатки. Правила сокращённого умножения с использованием дополнения не дают прямого указания цифр десятков D и цифр единиц E результата. Они не охватывают примеров умножения младших множителей менее 5.
«на пальцах»
Приведённые выше линейные правила сокращённого умножения можно демонстрировать на пальцах двух рук.
Вычисление «на пальцах» AxB. (Учебная игра).
Повернём руки ладонями к себе. Пронумеруем пальцы левой и правой руки числами от 6 до 10 снизу вверх.
Соединим два пальца с номером A на левой руке и номером B на правой руке, соответствующие множителям A x B решаемого примера.

Верхними пальцами назовем те пальцы, которые выше пальца A на левой руке, и выше пальца B на правой руке.
Нижние пальцы те, которые включают отмеченный палец и те, у которых номера меньше.
Применяем правило:
Десятки D произведения AxB равны сумме «нижних» пальцев двух рук.
Единицы E ответа равны произведению «верхних» пальцев левой руки на «верхние» пальцы правой руки.
Пример. 7x8. Отметим 7 – на левой руке второй снизу палец. Отметим 8 – на правой руке третий снизу палец.
На левой руке снизу 2 пальца, на правой руке внизу 3 пальца, поэтому десятки D=2+3=5.
На левой руке сверху 3 пальца, на правой руке сверху 2 пальца, поэтому единицы E=3x2=6. Ответ 7x8=[D;E]=56.
Пример. 6x8. Отметим 6 – на левой руке второй снизу палец. Отметим 8 – на правой руке третий снизу палец.
На левой руке снизу 1 палец, на правой руке внизу 3 пальца, поэтому десятки D=1+3=4.
На левой руке сверху 4 пальца, на правой руке сверху 2 пальца, поэтому единицы E=4x2=8. Ответ 6x8=[D;E]=48.
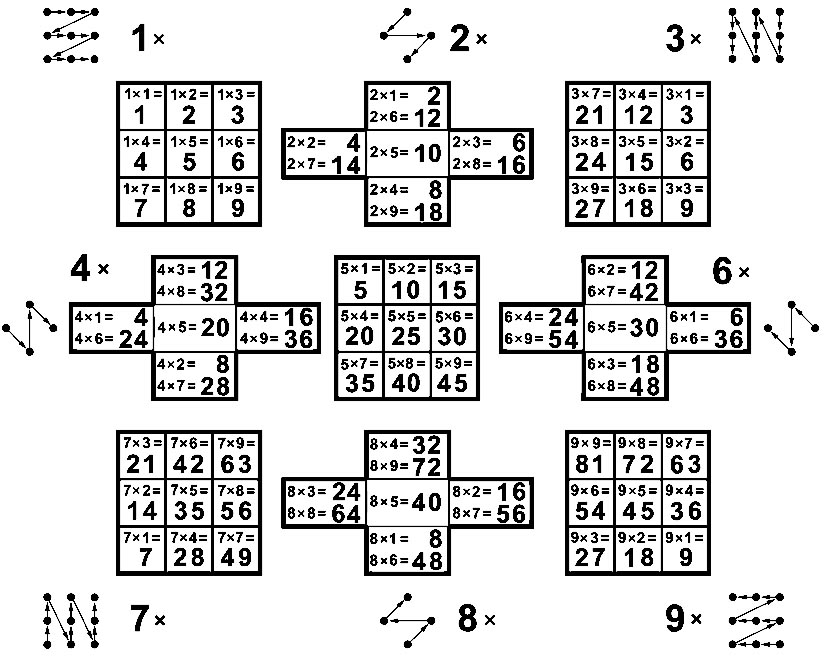
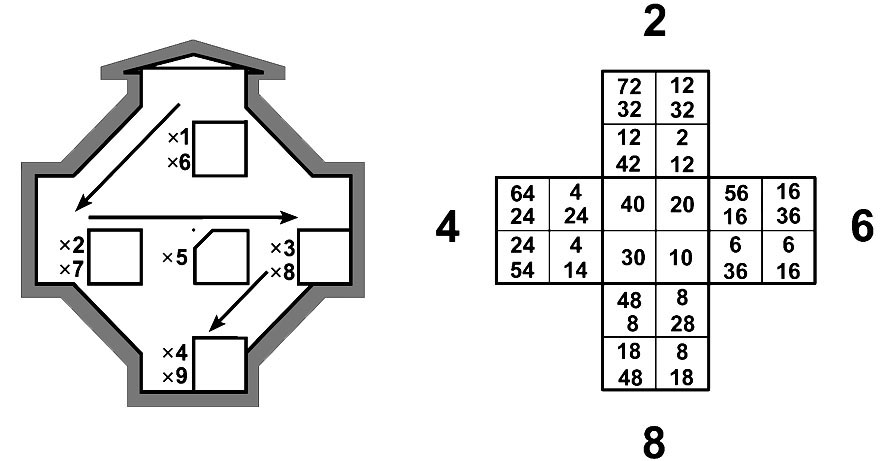
Таблица умножения Пифагора в формате девятилистника
Квадратная таблица Пифагора – не единственный возможный формат расположения произведений множителей. Существует специальный формат таблицы умножения – девятилистник, позволяющий по известным множителям A и B явно указать цифры D и E произведения AxB.
Каждый лист умножения представляет собой Т-матрицу, в ячейках которых разложим карточки с примерами умножения.
Структурное правило девятилистника требует, чтобы пример AxB=[D;E] был размещён на листе A в ячейке E.
Взаимное расположение разных листов умножения также подсказано строением Т-матрицы.
Последовательность чтения результатов на листе с номером A задаёт ломаная линия «A-молнии», состоящая из стрелочек-указателей. Каждая стрелочка на листе A соответствует примеру сложения A+B=[D;E], она ведёт от числа B к единицам E суммы A+B. (см. таблица сложения).
Чтобы не размещать на чётных листах по два примера в одной ячейке, можно взять две Т-матрицы. Примеры 2x5=10, 4x5=20, 6x5=30, 8x5=40 оказываются на числовой плоскости в ячейке 0 вне Т-матрицы. (Центр чётного листа можно использовать для компактности рисунка).
Модели таблицы умножения
Планетарная модель - «вращение планет» на девятилистнике умножения
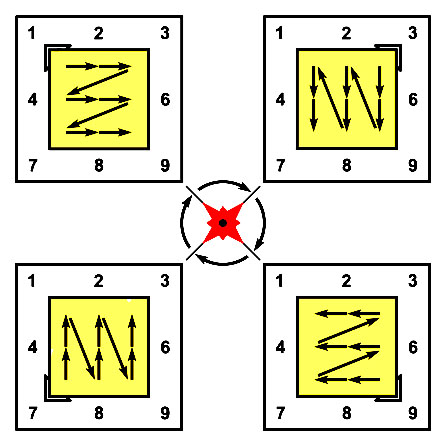
Сравнение линий молнии показывает, что на нечётных листах 1, 3, 7, 9 мы наблюдаем одну и ту же фигуру нечётной молнии в разных положениях поворота. Фигура молнии перемещается с одного листа на другой как твёрдое тело. Если задать траекторию перемещения между листами девятилистника в виде окружности, то нечётную молнию можно представлять как планету, облетающую центральное светило.
За время поворота по орбите вокруг центрального солнца «планета» – нечётная молния поворачивается вокруг своей оси на такой же угол. Любопытно, что планета всегда повернута к солнцу одной и той же стороной, как и Луна при вращении вокруг Земли. Числа на неподвижной Т-матрице листа умножения указывают постоянные направления на «далёкие звезды».
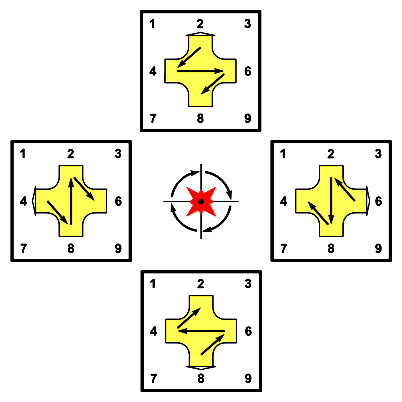
В таблице умножения на девятилистнике есть вторая «планета» – чётная молния, которая показана на чётных листах. Она поворачивается не только вокруг светила, но и вокруг своей оси.Модель, показывающая вращение молний на листах девятилистника умножения, названа моделью планетарного вращения единиц в таблице умножения. Впервые опубликована в 1999 г. (В.Б. Творогов, патент РФ № 2139574). Крылатая фраза «И все-таки она вертится!» – относится не только к Земле как планете солнечной системы, но и к нашей десятичной таблице умножения, в которой мы видим удивительные аналогичные явления.
Цифровые вертушки
на Т-матрице
Конструкция цифровой вертушки состоит из двух плоскостей, на которых нарисованы Т-матрицы и, если необходимо, другие фигуры. Через центры матриц проходит ось вращения, перпендикулярная их плоскостям. Дальняя от нас плоскость неподвижна, она называется основной плоскостью или основой. На основной плоскости размещают числовые результаты умножения (или только единицы результатов). Можно использовать прозрачную плоскость пропеллера цифровой вертушки или сделать на поворачиваемой плоскости вырезы, через которые видны числа на основной плоскости.
Для базовой конструкции вертушки потребуется два разных пропеллера цифровой вертушки (1) с рисунком нечетной молнии и (2) с рисунком чётной молнии. Узлы молнии пронумерованы по порядку появления на ломаной линии молнии 1-2-3-4…
В исходном положении молний мы видим 1-й лист (нечётная молния) и 2-й лист (чётная молния) девятилистника умножения. Четыре положения поворота пропеллера показывают разные листы умножения. Начальный узел молнии, нарисованный на пропеллере, указывает число A на основной Т-матрице. (Это – постоянный множитель A для всех примеров умножения на листе).
Ломаная линия из указателей A-молнии, изображённая на пропеллере, позволяет прочитать последовательные результаты умножения (Ax1); (Ax2); …; (Ax9).
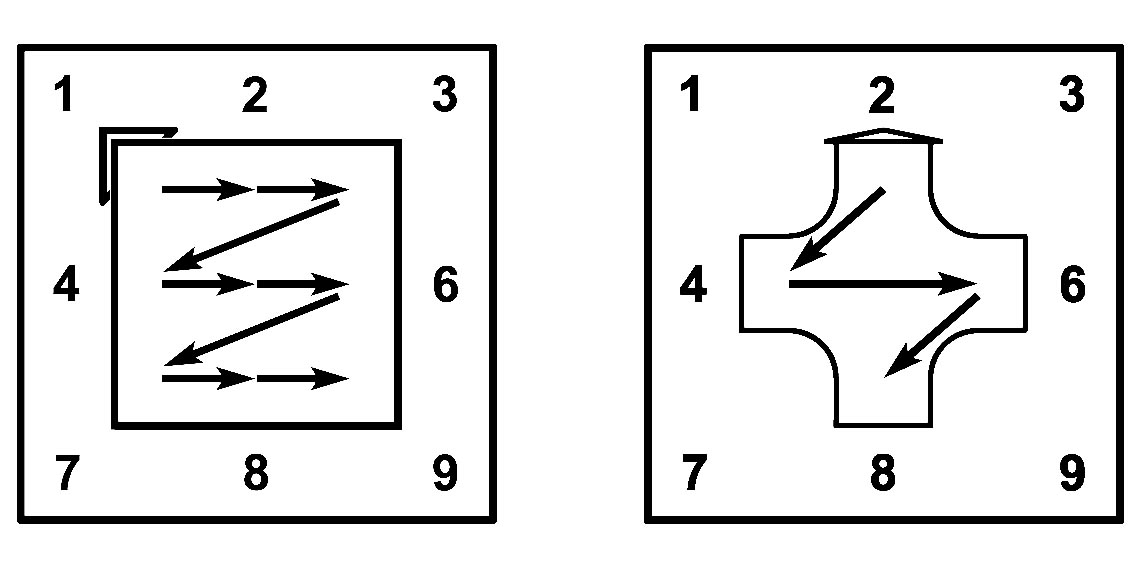
Правило единиц умножения на цифровой вертушке. (Универсальное правило)
Цифра единиц E (A x B) находится на A-молнии возле её узла с номером B.
Имеются алгоритмы определения единиц произведения на цифровой вертушке.
-
Метод неподвижного наблюдателя. (A не равно 5).
Берём молнию той же чётности, что и число A.
Шаг 1. Отмечаем фишкой узел 1-молнии с номером B.
Шаг 2. Поворачиваем пропеллер вертушки так, чтобы начальный узел молнии указывал число A на основной Т-матрице. (Теперь 1-молния превратилась в A-молнию).
Переносим фишку с пропеллера на основную Т-матрицу. Фишка показывает цифру единиц E произведения AxB.
-
Метод карусели. (A не равно 5).
Представим себе, что мы стоим в центре пропеллера цифровой вертушки и поворачиваемся вместе с ним.
Берём молнию той же чётности, что и число A.
Шаг 1. Поворачиваемся вместе с пропеллером вертушки лицом к числу A на основной Т-матрице. Отмечаем фишкой узел молнии с номером B.
Шаг 2. Переносим фишку с пропеллера на Т-матрицу и возвращаемся в исходное положение.
Фишка на основной Т-матрице показывает цифру единиц E произведения AxB.
Цифровые вертушки впервые описаны в патенте РФ (В.Б. Творогов. патент РФ №2139574, 1999 г., Вращающаяся таблица умножения).
Цифровые вертушки представляют собой инструменты счёта с новым принципом действия – поворотом луча на Т-матрице.
При вычислениях в уме человек визуально представляет геометрические элементы, наблюдаемые на цифровой вертушке. Расчёт выполняется путём геометрического построения на Т-матрице, итогом которого являются цифры произведений [D;E], (правила десятков приведены далее). На девятилистнике действует принцип – «место расположения определяет результат».
Вращающаяся таблица умножения
 Компактное
представление каждого листа умножения (кроме 5-го) в формате Т-матрицы
демонстрирует цифровая вертушка, получившая название вращающейся
таблицы умножения. На пропеллере прорезаны окошки для наблюдения
за числами результатов. На основной плоскости вращающейся таблицы
умножения записаны произведения – десятки и единицы примеров
умножения. При поворотах пропеллера меняются числа в окошках.
Компактное
представление каждого листа умножения (кроме 5-го) в формате Т-матрицы
демонстрирует цифровая вертушка, получившая название вращающейся
таблицы умножения. На пропеллере прорезаны окошки для наблюдения
за числами результатов. На основной плоскости вращающейся таблицы
умножения записаны произведения – десятки и единицы примеров
умножения. При поворотах пропеллера меняются числа в окошках.
Чтобы охватить все примеры таблицы Пифагора, нужны две цифровые вертушки - нечётная и чётная, в зависимости от чётности первого множителя A. На пропеллере нечётной вертушки изображена нечётная молния, а на пропеллере чётной вертушки нарисована чётная молния.
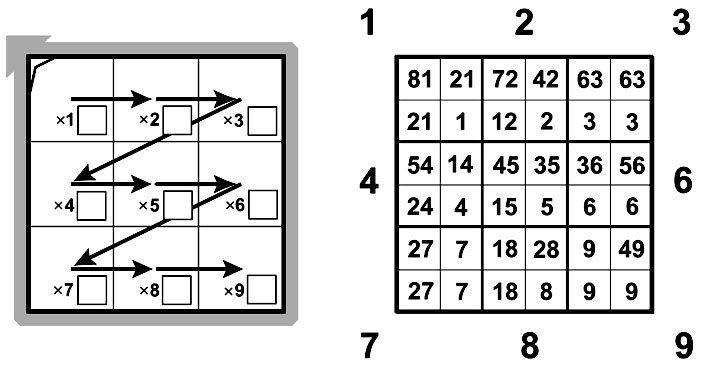
Последовательность чтения результатов умножения показывает линия из стрелочек – «молния» Т-матрицы. Для 1-го листа умножения молния показывает порядок возрастания чисел: слева направо в строке (+1) и сверху вниз по строкам (+3).
Последовательность чтения результатов 2-го листа (умножение на 2) задаёт «чётная молния», указывающая на следующее по величине чётное число Т-матрицы.
Повороты пропеллера позволяют прочитать в окошках пропеллера все произведения AxB=[D;E]. Место расположения карточки с примером определяется местом числа E на основной Т-матрице (структурное правило девятилистника умножения).
Ступенчатые 3D модели таблицы Пифагора
Ступенчатая модель A-листа умножения представляет собой лист девятилистника умножения, ячейки которого подняты над основанием Т-матрицы на высоту в D этажей, где D – величина десятков произведения AxB=[D;E]. Ступенчатые модели исследовал В.Б. Творогов (Наглядная арифметика и технология быстрого счёта. - М.: Либроком, 2011.).
Указывая одну точку на ступенчатой модели, мы получаем одновременно две цифры: цифру E как проекцию на Т-матрицу, цифру D как высоту этажа над основанием.
Ступенчатые модели предлагают удобные компактные визуальные образы, мгновенно подсказывающие результаты умножения в технологии быстрого счёта. Обратим внимание на то, что визуальный образ A-листа ступенчатой модели появляется в визуальной памяти целиком, а затем мы считываем с этого образа конкретные цифры, основываясь на соглашениях стандарта Т-матрицы для устного счёта. Похожий процесс в мышлении происходит, когда мы представляем карту гористой местности, а затем, прокладываем на ней маршрут к заданной точке.
Умножение.
Цифровые правила единиц
Правила для единиц, использующие поворот луча на Т-матрице
Обозначим буквой R функцию поворота на Т-матрице радиального луча на прямой угол по часовой стрелке. Девятилистник умножения демонстрирует геометрические цифровые законы для единиц. Пусть A натуральное однозначное число. Тогда единицы
E (3 x A) = R (A), E (9 x A) = R2 (A), E (7 x A) = R–1 (A).
Эти формулы являются цифровыми правилами единиц для умножения на 3, 9 и 7.
Два поворота дают дополнение R2 (A) = A*. Можно записать E (9 x A) = R2 (A) = A*.
Правила единиц, использующие поворот луча, являются универсальными для таблицы умножения.
Цифровое правило можно представить как геометрический алгоритм указания цифры единиц.
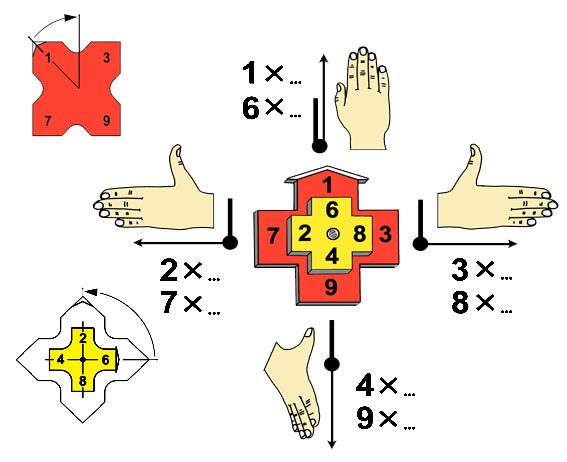
Правило единиц для умножения на 3 является правилом правой руки.
Допустим, мы находимся в центре Т-матрицы и смотрим на множитель A. Тогда цифра единиц E (3 x A) находится справа от нас.
Чтобы получить цифру единиц E (3 x A), нужно повернуть радиальный луч множителя A на Т-матрице на прямой угол по часовой стрелке.
Правило умножения на 3 удобно показывать правой рукой, отставив в сторону большой палец. Кладём правую ладонь на центр Т-матрицы и поворачиваем руку так, чтобы большой палец показывал множитель A. (Если поворачивать руку не удобно, поверните листок с рисунком). Тогда остальные пальцы укажут цифру единиц E.
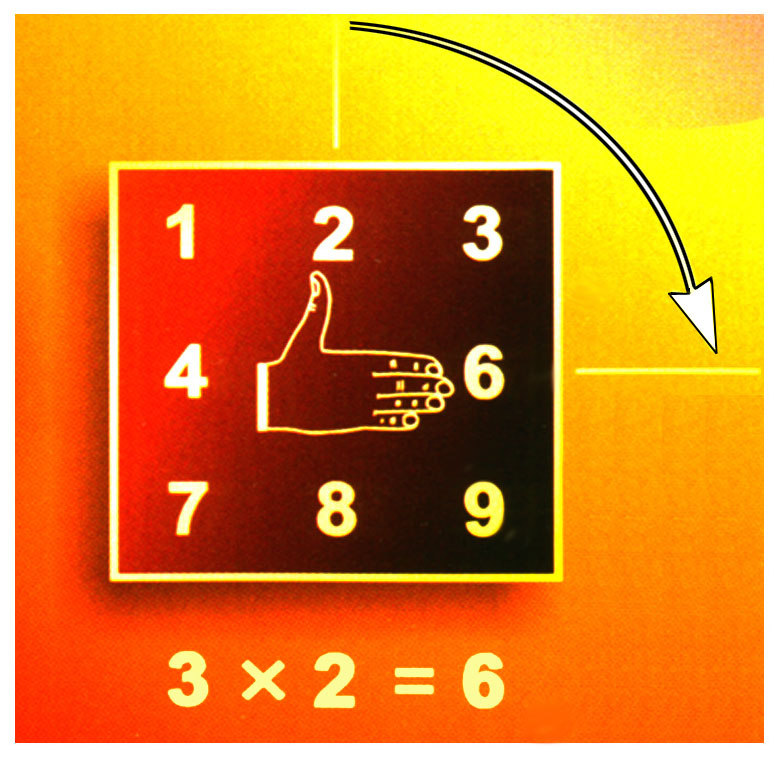
Правило единиц для умножения на 7 является правилом левой руки.
Допустим, мы находимся в центре Т-матрицы и смотрим на множитель A. Тогда цифра единиц E (7 x A) находится слева от нас.
Чтобы не перепутать соответствия того, какая рука относится к какой цифре, достаточно встать в центр Т-матрицы и повернуться лицом к цифре 1. Тогда 3 будет видна справа, а цифра 7 окажется слева от начального луча зрения на цифру 1.
Пусть A является чётным числом. Тогда
E (6 x A) = A, E (2 x A) = R–1 (A), E (4 x A) = R2 (A), E (8 x A) = R (A).
Эти формулы являются цифровыми правилами единиц для чётных множителей, использующими поворот луча на Т-матрице.
Чтобы определить величину уголка для каждой чётной цифры, нужно на Т-матрице повернуться, глядя вдоль радиального луча числа 6. Тогда 8 окажется справа, 2 – слева, а 4 – позади нас.
Правила единиц, использующие молнии
Правила единиц, использующие повороты нечётной и чётной молнии Т-матрицы
Решим пример A x B = [D; E] с помощью цифровой вертушки. (Далее исключаем случай A=5). Берём цифровую вертушку с пропеллером, на котором изображена молния той же чётности, как и A.
Шаг 1. Устанавливаем фишку на узел U=B выбранной молнии.
Шаг 2. Поворачиваем пропеллер вместе с фишкой так, чтобы начальный узел молнии указал на число A. Теперь молния МA на пропеллере совпадёт с A-молнией на Т-матрице. Фишка указывает на Т-матрице цифру единиц E(AxB).
E ( A x B ) = МA ( B ).
Правила единиц, использующие уголки
Решаем пример AxB=[D;E] геометрическим способом, используя две планки, образующие фиксированный угол.
Для цифровой вертушки на Т-матрице возьмём пропеллер с нарисованными на нём уголками. Каждый уголок представляет собой жёсткую фигуру с двумя планками – (1) короткой и толстой, и (2) длинной и тонкой. Величина угла выбирается в строгом соответствии с множителем A (см. рис.).
Вершина уголка надевается на ось в центре Т-матрицы. Поворачиваем уголок так, чтобы короткая планка указала на множитель B. Тогда длинная планка укажет цифру единиц E произведения AxB.
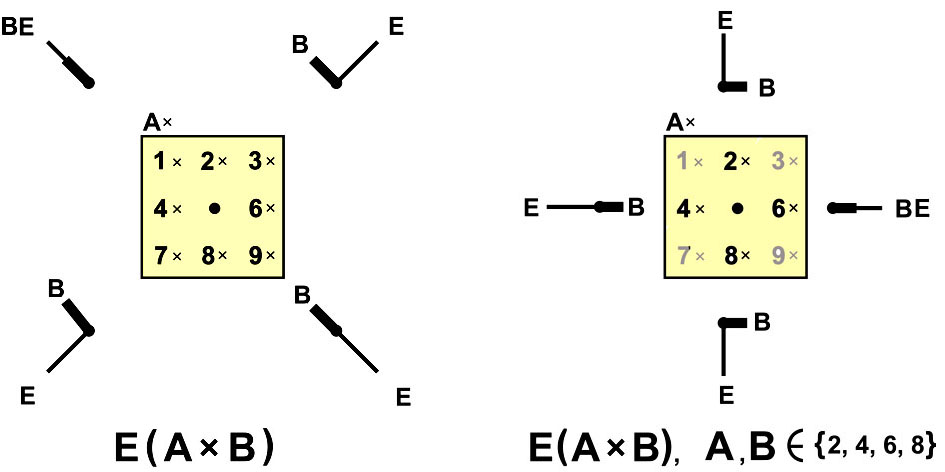
Цифровая вертушка с уголками похожа на часы с двумя стрелками. Отличие в том, что угол между стрелками на вертушке типа «часов умножения» не меняется, он зависит только от множителя A. Решение примеров умножения на 3 показано на рисунке.
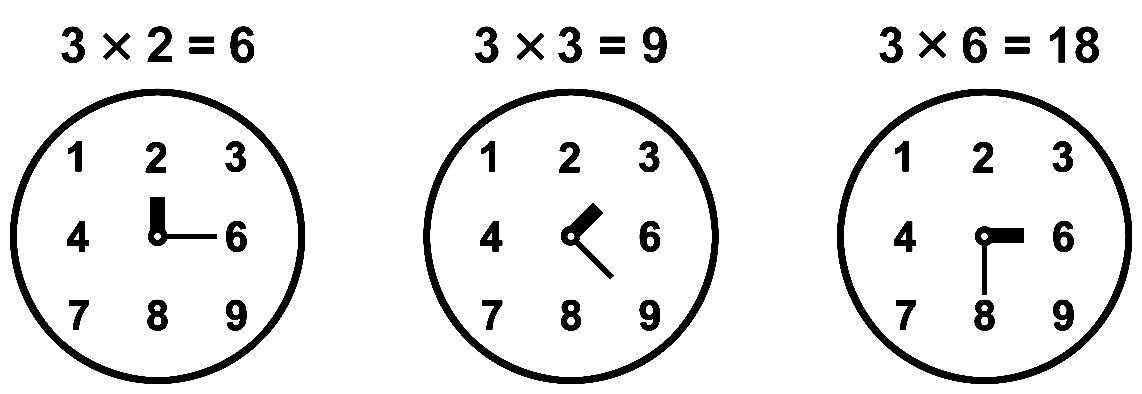
Если A – нечётное число, не равное 5, то B – любое число Т-матрицы. У числа B=5, находящего в центре вращения, радиального луча не существует. Число B=5 указано центральной точкой, которая при поворотах остаётся на постоянном месте.
Если A – чётное число, тогда B – так же должно быть чётным числом.
Рекомендация. Решая пример AxB, на первое место нужно поставить нечётное число, если оно имеется в произведении.
Правила десятков
Правила десятков и инверсии на указателях единиц
Универсальное правило десятков. Десятки D(AxB) равны числу инверсий при движении по указателям A-молнии от начального узла до узла с номером B
![]()
где I (c) – функция инверсии, равная 1, если на указателе молнии между узлами (c, c+1) есть инверсия, и равная 0 в остальных случаях.
Инверсия на указателе B->E имеется только тогда, когда B>E.
Правила десятков, использующие границы десятков между ячейками Т-матрицы.
На выбранном листе девятилистника умножения записаны произведения AxB=[D;Е]. В соответствии со структурным правилом девятилистника карточка примера AxB=[D;Е] размещается в ячейке E.
Множество ячеек с одинаковыми цифрами десятков D произведения называются D-областью десятков.
Проведем между соседними ячейками с разными числами десятков D разграничительные линии – границы. Возможны кратные линии границы (двойные или тройные).
Линия A-молнии показывает последовательность чтения результатов Ax1=[0; A], Ax2=[D2;Е2], ..., AxB=[DB; ЕB].
Алгоритм расчёта десятков на Т-матрице по известным линиям границ десятков.
Для того чтобы узнать величину десятков D произведения AxB, нужно пройти на A-листе по указателям молнии от её начала до узла с номером B, и подсчитать число пересечений границ.
Из универсального правила десятков следует, что число инверсий равно числу пересечений границ десятков.
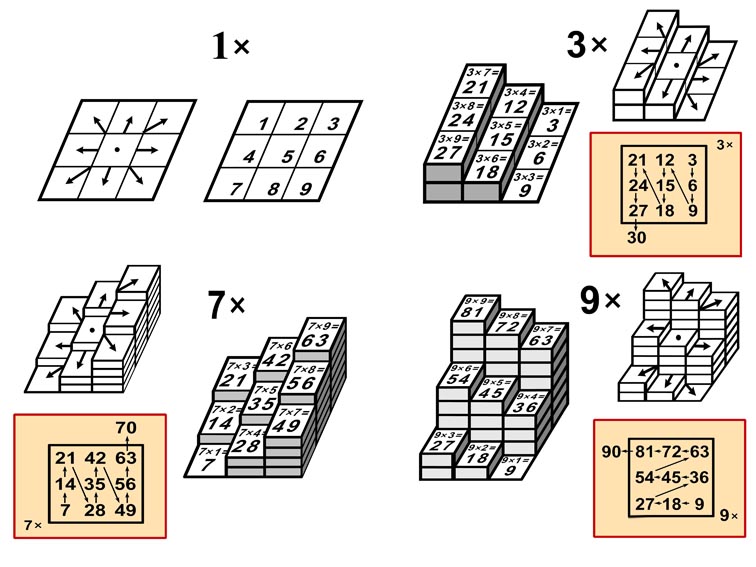
На рисунке показаны границы десятков нечётных листов 1, 3, 7, 9.
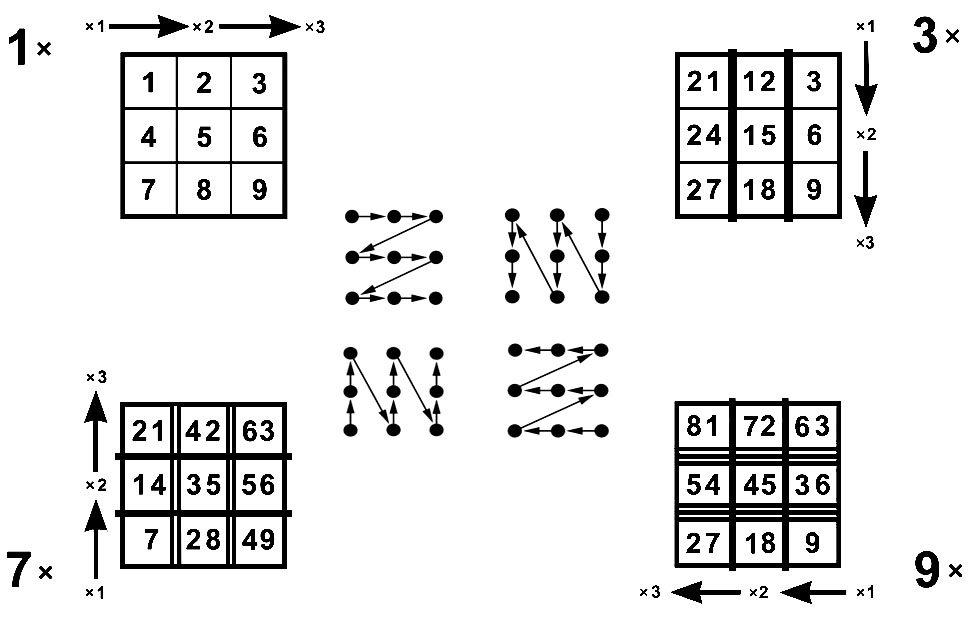
Лист 1 не имеет границ десятков, так как здесь все результаты 1 x A = A < 10 и D=0.
Лист 3 имеет вертикальные границы десятков, разделяющие столбцы Т-матрицы. Каждый шаг налево увеличивает десятки на 1. В правом столбце десятки равны нулю, произведения 3 x 4 = 12, 3 x 5 = 15, 3 x 6 = 18 имеют десяток D=1.
В левом столбце все произведения 3 x 7 = 21, 3 x 8 = 24, 3 x 9 = 27 имеют десяток D=2.
Лист 7 отличается тем, что каждый шаг вверх увеличивает десяток на 1, и каждый шаг направо увеличивает десяток на 2. Поэтому горизонтальные границы - однократные, вертикальные границы между ячейками - двукратные.
Лист 9 замечателен тем, что все его примеры 9xB = [D;Е] подчиняются правилу: десятки на единицу меньше множителя D = B - 1. На девятом листе вертикальные границы - однократные, горизонтальные границы - трехкратные.
Для того чтобы визуально запомнить расположение границ десятков, полезно иметь перед глазами ступенчатые модели каждого листа умножения.
Перемещаясь по A-молнии от её начала до нужного нам множителя B, нужно подсчитать встречающиеся границы.
Переход через границу десятков изменяет D на величину кратности границы.
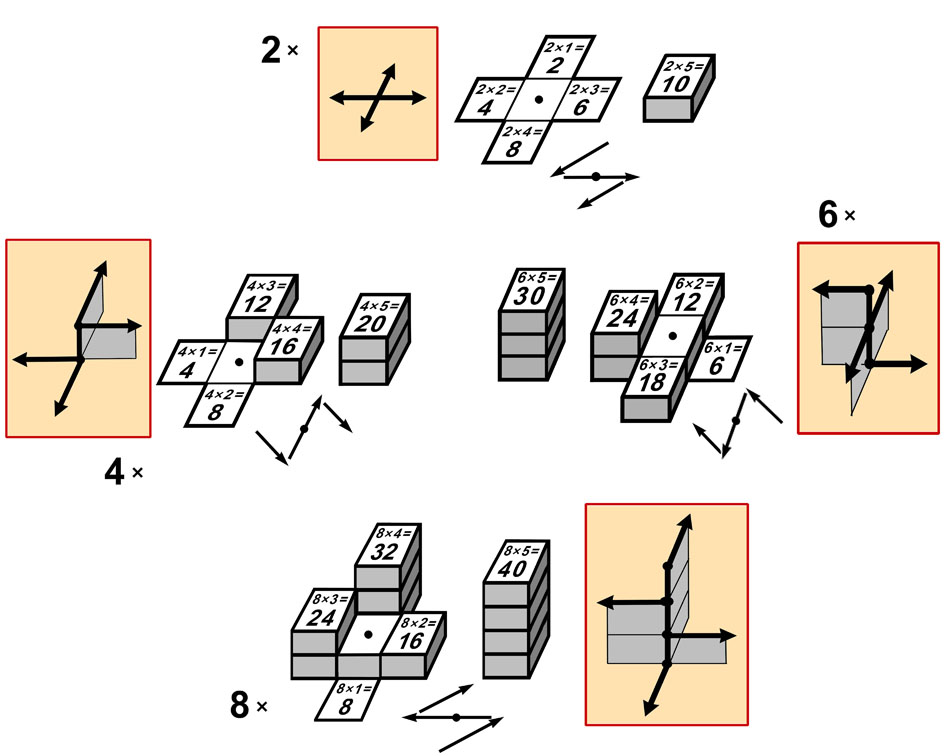
Границы десятков чётных листов умножения показаны для младших узлов чётной молнии U из множества {1, 2, 3, 4}.
Для старших узлов чётной молнии U из множества {6, 7, 8, 9} формат границы десятков повторяется.
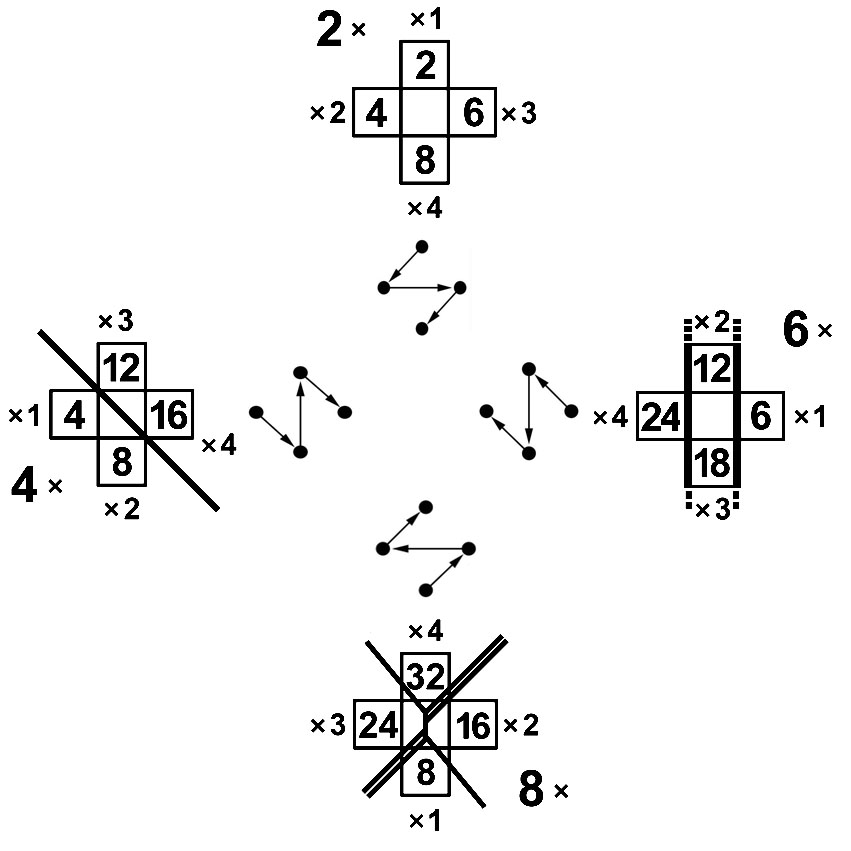
На чётных листах последовательность чтения результатов задаёт соответствующая чётная молния.
Лист 2 состоит из двух частей. Младшая часть с примерами 2 x 1 = 2, 2 x 2 = 4, 2 x 3 = 6, 2 x 4 = 8, имеет цифры десятков D=0, старшая часть листа приподнята на один этаж вверх D=1.
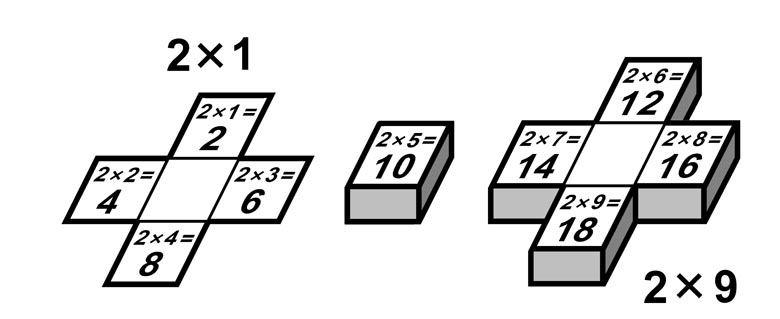
На листе 4 переход через главную диагональ направо или вверх увеличивает величину десятков на 1.
Заметим, что примеры 4 x 5 = 20, 4 x 6 = 24 и 4 x 7 = 28 находятся в одной зоне десятков D = 2.
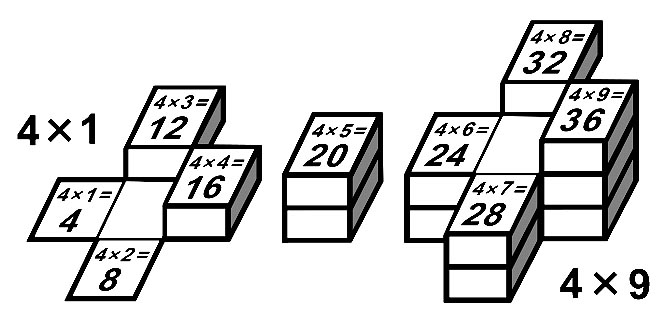
Лист 6 похож на лист 3, но на нём используются только чётные ячейки. Каждый шаг налево по Т-матрице увеличивает десяток на 1.
Нужно помнить, что примеры 6 x 5 = 30 и 6 x 6 = 36 находятся в одной зоне десятков D = 3.
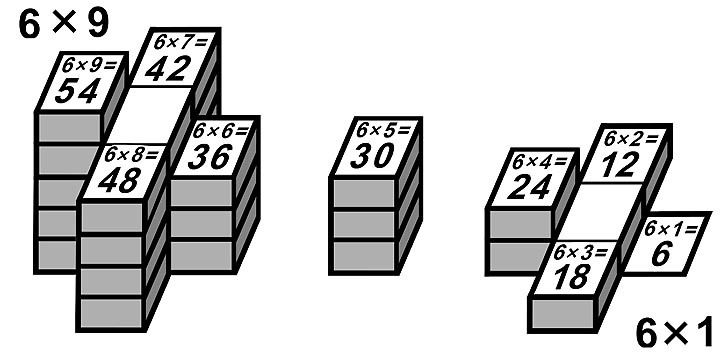
На листе 8 каждый шаг по 8-ой молнии увеличивает десяток на 1, за исключением перехода от 8 x 5 = 40 до 8 x 6 = 48.
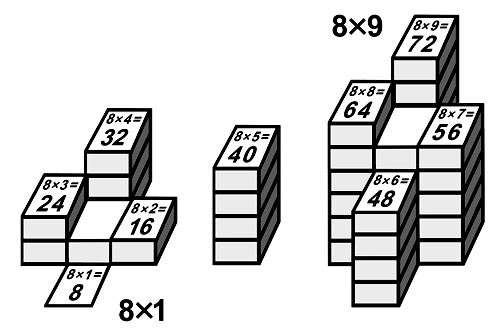
В технике визуального счёта можно упростить применение алгоритма десятков. От первого узла молнии до узла с номером B можно перемещаться по любому маршруту, не повторяя поворотов молнии. Ступенчатая модель подскажет правильный результат для десятков D в конечной точке маршрута.
Каждый маршрут на Т-матрице эквивалентен какому-либо варианту вычисления.
в устном счёте
Варианты использования таблицы Пифагора в устном счёте
В настоящее время известно несколько отличающихся между собой концепций включения таблицы Пифагора в устные вычисления. В каждой из концепций присутствует теоретическое обоснование, выдвигаются свои требования к человеку-вычислителю по владению некоторыми специальными стандартными навыками.
В каждой концепции применения таблицы Пифагора имеются ответы на следующие вопросы:
* В каком объеме следует заучивать таблицу Пифагора,
* На какую терминологию, и какие утверждения нужно опираться,
* Какие цифровые правила следует изучать и применять, решая задачи умножения,
* Какие геометрические схемы обязательны для применения в устном счёте,
* В каком сочетании используются аудиомоторная память и визуальная память.
Дадим краткий обзор этих концепций.
* На первое место поставим традиционный устный вербальный счёт, известный каждому школьнику, заучивания словами всех результатов таблицы Пифагора от 1x1 до 10x10. На самом деле, заучиваются лишь примеры от 2x2 до 9x9. (Умножение на 1 тривиально, а умножение на 10 - это приписывание нуля справа). При каждой встрече с парой однозначных множителей нужно воспроизвести словесную фразу типа «семью восемь – пятьдесят шесть». Умножение многозначных чисел выполняется поразрядно в десятичной записи чисел (метод умножения «крестиком»). Комментарии к этой стандартной концепции излишни.
* Линейная система цифровых правил (см. выше), известная со средних веков (и, есть гипотеза, со времен пифагорейцев), позволяющая преобразовать пример с однозначными множителями более 5 к дополнительным множителям менее 5.
Строго говоря, в этой системе счёта можно ограничиться заучиванием только младших произведений от 2x2 до 5x5. На практике эта рекомендация не соблюдается, ученики заучивают подряд все примеры до 9x9.
* Система Я. Трахтенберга цифровых правил устного счёта предъявляет требования к человеку-вычислителю, чтобы он знал наизусть и применял для получения цифр десятков D и единиц E не только величины множителей A и B, но и их двойные значения 2A, пятикратные значения 5A и половинные значения A/2. Предлагаются линейные формулы вычисления разрядов десятков и единиц. Младшие множители до 4x4 не охватываются эффективными правилами, поэтому должны заучиваться наизусть.
Сейчас система Я. Трахтенберга представляет лишь исторический интерес. Концепция наглядной арифметики В. Б. Творогова оказывается эффективнее системы Я. Трахтенберга по всем критериям сравнения.
* Система цифровых правил наглядной арифметики, где используются геометрические алгоритмы, демонстрируемые на телефонной Т-матрице и числовой плоскости. Нужная цифра десятков D и единиц E произведения однозначных множителей A×B=[D;E] указывается как точка в некоторой конфигурации.
Алгоритмы наглядной арифметики строятся на основе стандарта Т-матрицы для устного счёта. Согласно этому стандарту, человек-вычислитель должен знать
(1) где находится каждая цифра на Т-матрице, указывая её радиальным лучом, и
(2) какая цифра находится в заданной ячейке Т-матрицы.
Из элементарных компонент строятся молнии Т-матрицы, показывающие порядок чтения результатов на A-листе умножения.
Цифровые правила для единиц и десятков позволяют указать числовые решения для всех примеров умножения таблицы Пифагора.
Геометрическая интерпретация арифметических действий удобна для технологии быстрого счёта, так как после указания точки на геометрической схеме уже не требуется называть числа словами, поэтому время вычислений сокращается.
"двух камешков"
для умножения
до 10×10
Геометрический алгоритм «двух камешков» для умножения от 5x5 до 10x10.
Простой и очевидный алгоритм «двух камешков» позволяет геометрически решить пример таблицы умножения с множителями от 5 до 10. Существует гипотеза, что этот алгоритм применяли пифагорейцы, выполняя расчёты на абаке.
Ищем решение в виде AxB=[D; E], где D -десятки, E - единицы произведения.
Полные десятки – это базовые числа. Линии координат, проходящие через точку (10;10) будем называть базовыми линиями.
Дополнение числа до полного десятка обозначим звездочкой A*=10-A, B*=10-B.
Геометрическое построение. Внутри квадрата 10x10 изобразим прямоугольник AxB, отметив точку с координатами (A; B). Дополнительный прямоугольник находится между точками (A; B) и (10; 10).
Разрежем прямоугольник AxB на два прямоугольника той же суммарной площади, один из которых покажет десятки, другой – единицы. Передвигая разрезанные фигуры, получим прямоугольник площади Dx10, одна сторона которого равна десяткам D, и прямоугольник площади E=A*xB*, где E - единицы произведения AxB. (Левая иллюстрация).
На правой базовой координатной линии отмечаем камешком 1 величину множителя A – точка (1) - кружок.
На нижней базовой
координатной линии отмечаем камешком 2 величину множителя B
– точка (2) - квадратик.
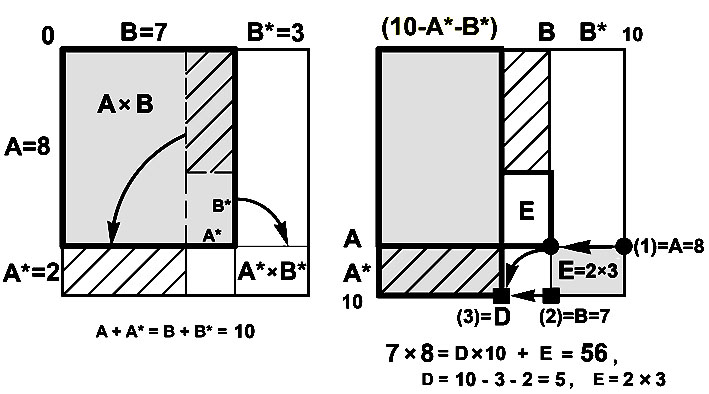
1-й шаг. Перемещаем 1-й камешек A налево на величину B*.
Теперь этот камешек отмечает прямоугольник от точки (A;B) до точки (10;10),
его площадь равна числу единиц E = A* x B* произведения A x B.
2-й шаг. Вычитаем из отрезка длины 10 величины A* и B*. Для этого строим окружность с центром во 2-ом камешке радиусом A*.
Перемещаем 2-й камешек из точки (2) налево в точку (3) пересечения окружности и горизонтальной линии.
Длина отрезка от точки (10; 0) до (10; D) равна D = 10 – A* – B*, где D – число десятков произведения A x B.
В итоге D = 10 – A* – B* = A – B*.
Пример. 9 x 9 = ? A = 9, B = 9. A* = 10 – 9 = 1; B* = 10 – 9 = 1.
Е = A* x B* = 1 x 1 = 1. D = A – B* = 9 – 1 = 8. Ответ: 9 x 9 = 10 x 8 + 1 = 81.
Пример. 7 x 8 = ? A = 7, B = 8. A* = 10 – 7 = 3; B* = 10 – 8 = 2.
Е = A* x B* = 3 x 2 = 6. D = A – B* = 7 – 2 = 5. Ответ: 7 x 8 = 10 x 5 + 6 = 56.
"двух камешков"
для умножения
от 10×10 до 15×15
Геометрический алгоритм «двух камешков» для умножения от 10x10 до 15x15.
В случае, когда множители A и B превосходят 10, геометрическое построение выполняется на координатной сетке правее и ниже точки 10x10 (рис.). Алгоритм «двух камешков» прежний, отличие лишь в том, что камешки смещаются направо.
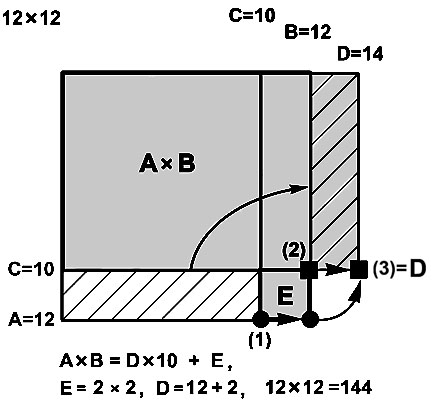
Ищем решение в виде X x Y = [H; D; E].
Для множителей из окрестности базовой точки (10;10) величина сотен H=1.
Представим множители X x Y в виде X = (10+A) и Y = (10+B).
На базовых линиях координат отмечаем камешками величины двух множителей: (10+A) – точка (1) – кружок и (10+B) – точка (2) – квадратик.
Алгоритм.
1-й шаг. Перемещаем 1-й камешек направо на величину B. Теперь этот камешек отмечает модельный прямоугольник
от точки 10 x 10 до точки (10 + A) x (10 + B).
Число единиц E произведения X x Y равно площади модельного прямоугольника E=AxB.
2-й шаг. Строим отрезок, длина которого равна сумме (A + B).
Перемещаем 2-й камешек направо в точку пересечения окружности радиуса A с центром в точке (2) и горизонтальной линии – это точка (3).
Длина отрезка от точки (10; 10) до (10; D) равна D = A + B, где D – число десятков произведения X x Y.
Пример. 12x12 = ? A = 2, B = 2. Е = AxB = 2x2 = 4. D = A + B = 2 + 2 = 4.
Ответ: 12x12 = [1; 4; 4] = 144.
Для умножения в уме 12 x 12 достаточно представить в своем воображении модельный квадрат 2x2.
Число единиц E равно площади квадрата 2x2. Число десятков равно полупериметру модельного квадрата D=2+2=4.
12x13 = ? A = 2, B = 3. Е = AxB = 2x3 = 6. D = A + B = 2 + 3 = 5.
Ответ: 12x13 = [1; 5; 6] = 156.
Для умножения 12 x 13 минимальный визуальный образ – это модельный прямоугольник 2x3.
Если A£13 и B£13, тогда Е = (A* x B*) £ 9. Нормализация с переносом «лишних» десятков в старший разряд не требуется. Алгоритм умножения методом пифагоровых схем в диапазоне множителей A£13 и B£13 даёт точные цифры H, D и E.
Подробности см. в статье Творогов В.Б. Как пифагорейцы учили таблицу умножения.
таблицы Пифагора
Умножение от 5x5 до 15x15
Многие полагают, что умножение до 10 выполняется просто, а умножение чисел более 10 - сложнее. На самом деле, один и тот же алгоритм умножения от 5x5 до 10x10 действует без изменений в широком диапазоне от 5x5 до 15x15. Другими словами, мы должны решать примеры до 15x15 так же просто, как и примеры до 10x10.
Применим для расчётов метод пифагоровых схем.
Сформулируем общую теорему метода пифагоровых схем c базовыми числами (10; 10).
Разность SA=A–10 между A и базовым числом 10 называется смещением.
Терема. Пусть множители 5 ≤ A ≤ 15; 5 ≤ B ≤ 15. Ищем произведение в виде AxB = [H; D; E].
Тогда сотни H = 1; десятки D = SA + SB; единицы E = SA x SB.
На чертеже достаточно иметь прямоугольник со сторонами A и B.
Величина единиц E – это площадь модельного прямоугольника (с учётом знаков смещений).
Величина десятков D равна полупериметру (сумме двух сторон с учетом знаков смещений).
Алгоритм умножения на пифагоровой схеме с базой (10;10).
|
Подготовка |
Представим множители X x Y в виде X = (10 + A) и Y = (10 + B). Строим кратчайший маршрут между базой (10;10) и точкой множителей (X;Y).
|
|
Шаг 1. |
Перемещаемся от базового числа до точки, указанной множителями (X;Y). Одновременно подсчитываем изменение базовых десятков, меняя величину Do=10xH=10x1=10. Пифагоровы десятки (в итоге) равны D = Do + A + B = 10 + A + B = X + B или D = X + (Y – 10). (К первому множителю добавляем смещение второго множителя. Записываем в разряд десятков).
|
|
Шаг 2. |
Добавляем пифагоровы единицы E = A x B.
|
|
Ответ: |
X x Y = [ D; E ] = [ (X + (Y – 10) ); (A x B) ].
|
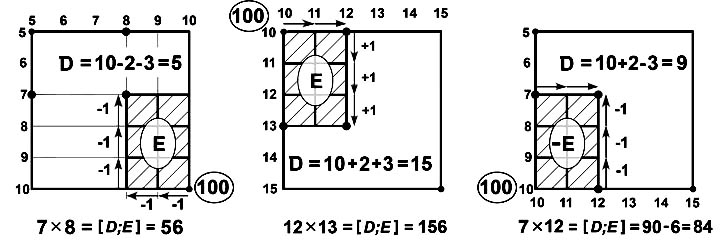
Преимущества метода пифагоровых схем по сравнению со стандартным умножением "крестиком" в том, что мы имеем:
(1) наглядную геометрическую схему ("пространство решений", где мы видим все соседние результаты);
(2) можем перемещаться по координатной сетке по горизонтальному или вертикальному направлению, что эквивалентно умножению "крестиком";
(3) можем перемещаться в диагональном направлении, меняя одновременно два множителя. (Перемещение по диагонали не имеет вычислительного эквивалента в методе умножения "крестиком".)
Справочная таблица для расчёта пифагоровых десятков в окрестности базы (10;10)
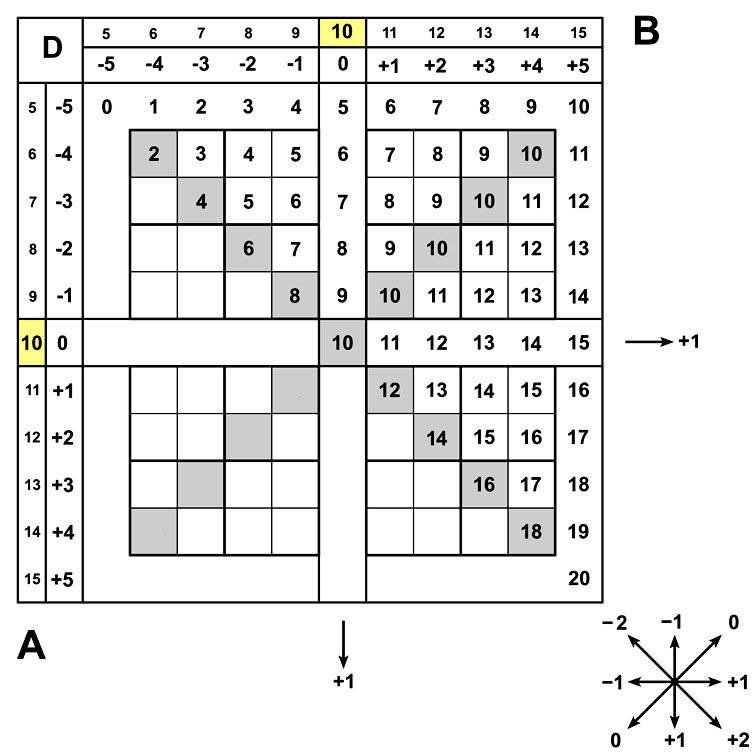
Пример. 9 x 13 = ? H=1. Множители X = 10 - 1, Y = 10 + 3. Смещение A = –1, B = 3.
Единицы Е = A x B = (–1) x 3 = –3.
Сотни и десятки: D = X + B = 9 + 3 = 12.
Ответ: 13 x 9 = [ (12); (-3) ] = 120 – 3 = 117.
Для умножения 9 x 13 достаточно представить в воображении прямоугольник 1x3, у которого базовая точка (10;10) находится в левом нижнем углу.
Пример. 6 x 14 = ? H=1. Множители X = 10–4, Y = 10+4. Смещение A = –4, B = 4.
Сотни H = 1. Десятки D = A + B = 4 – 4 = 0. Единицы Е = A x B = (–4) x 4 = –16.
Ответ: 14 x 6 = [1; 0; (-16)] = 100 – 16 = 84.
При расчётах методом пифагоровых схем главная работа заключается в том, чтобы вычислить пифагоровы десятки.
Не нужно следить за пифагоровыми единицами, так как они добавляются лишь при формулировании окончательного ответа. Это обстоятельство уменьшает сложность решения.
О методе расчёта см. статью "Визуализация устных вычислений с помощью пифагоровых схем".