Геометрические схемы умножения

двузначных чисел.

Первые шаги.

У пифагорейцев Древней Греции выделялся раздел, описывающий правила действия над числами, который назывался логистикой (Logisticm – счетное  искусство). Счет проводился, в основном, на счетной доске – абак – с помощью камешков.

Абак - это счётная доска, представляющая собой древнейший вычислительный инструмент. Расчёты проводились путём раскладывания камешков на размеченных линиях.

При раскопках на острове Саламин в 1848 г. найден гигантский абак, датируемый 300 г. до н.э., выточенный из мрамора в виде тонкой плоской пластины размерами 1,5 на 0,75 метра. На абаке проведены вертикальные борозды, разделяющие камешки с разными значениями (1, 5, 10, 50, 100, 500, 1000). Саламинский абак выделял и дробные значения ½, ¼. Полученные с помощью абака числа записывались в ионийской буквенной системе числовой нотации.

На абаке решались многочисленные практические задачи обмена денег разных государств. Древнегреческий Полибий (ок. 201 – ок. 120 г. до н.э.) в книге «История» привел замечание: «Придворные – как камешки на счётной доске: захочет счётчик, и они будут стоить один халк, а захочет – так и целый талант». (1_талант = 6000 халк).

Историки математики достаточно хорошо знают о том уровне теоретических достижений, которым владели учёные разных народов. Француз Герберт (940-1003), познакомившись с абаком, написал о нем в 982 году книгу, получившую известность в Европе. Реконструкцию методов древнегреческого умножения проводили известные математики Ван дер Варден, М.Я. Выгодский, А.В. Волошинов и др.

Тем не менее, нет практически никакой информации о технике устного счёта ни первых пифагорейцев, заложивших основы математических знаний, ни их последователей. Как пифагорейцы и их многочисленные ученики использовали свои знания о таблице умножения в устном счёте? Что заучивали наизусть, что вычисляли по простым алгоритмам в уме, что приходилось записывать? Прямого ответа на этот вопрос у историков математики нет. Полагаем, что неправильно переносить на всех учеников Древней Греции современный постулат о том, что каждый ученик должен заучивать все примеры умножения однозначных чисел от 1x1 до 10x10 как словесные фразы типа «дважды два – четыре». Почему возникают такие сомнения? В прямом заучивании фраз не используются очевидные геометрические знания:

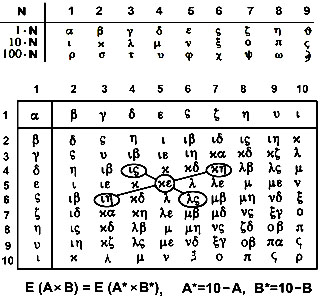
(1) представление результатов в виде квадратной таблицы умножения Пифагора;

(2) геометрическое определение умножения AxB как площади прямоугольника со сторонами A и B;

(3) знания о симметриях единиц в таблице умножения (см. рис.).

Используя современные знания, мы попытаемся приоткрыть завесу тайны в вопросе о том, какие сведения о таблице умножения пифагорейцы обязательно заучивали, и какие геометрические алгоритмы использовались для устного умножения.

Совокупность методов счёта, в которой используются геометрические симметрии таблицы Пифагора (дополнения чисел до полного десятка), будем называть пифагоровой системой счёта.

Минимально необходимый объем заучивания примеров умножения однозначных чисел в пифагоровой системе счёта ограничен множителями от 2x2 до 5x5. Остальные произведения старших множителей, величины которых более 5, вычисляются с использованием симметрии дополнения через младшие множители менее 5.

Малые множители

в пифагоровой

 системе счёта

Нет сомнения в том, что результат 2x2=4 у древнегреческих математиков  иллюстрировался квадратом со стороной 2, разрезанный на ячейки 1x1. Для запоминания 3x2=6 нет лучшего образа, чем прямоугольник со сторонами 2 и 3. Реконструируя систему устного счёта пифагорейцев, мы предполагаем, что обязательными для запоминания были площади прямоугольников от 2x2 до 5x5.

Прямоугольники, имеющие длины сторон 3 или 4 для надёжного запоминания следует разрезать на стандартные части

2x4 = 2x2+2x2,  3x4 = 3x3+3 = 3x3+1+2 = 10+2.

Множитель 4 можно представить как 4=5-1 , поэтому результат умножения на 4 можно сравнить с объемлющим прямоугольником со стороной 5x2=5+5=10.

4x2 = (5-1)x2 = 5x2-2 = 8,    4x3 = (5-1)x3 = 5x3-3 = 10+5-3 = 15-3=12,

4x4 = (5-1)x4 = 5x4-4 = 5x2+5x2-4 = 20-4 = 16.

Умножение на Ax5 решается правилом деления множителя пополам A/2, дающее число десятков.

"двух   камешков"

для умножения

от 5x5 до 10x10

Приведём описание алгоритма "двух камешков" для умножения величин от 5x5 до 10x10.

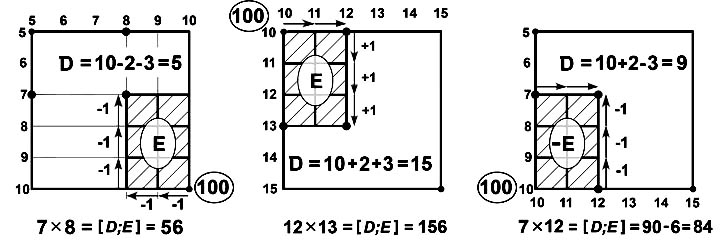
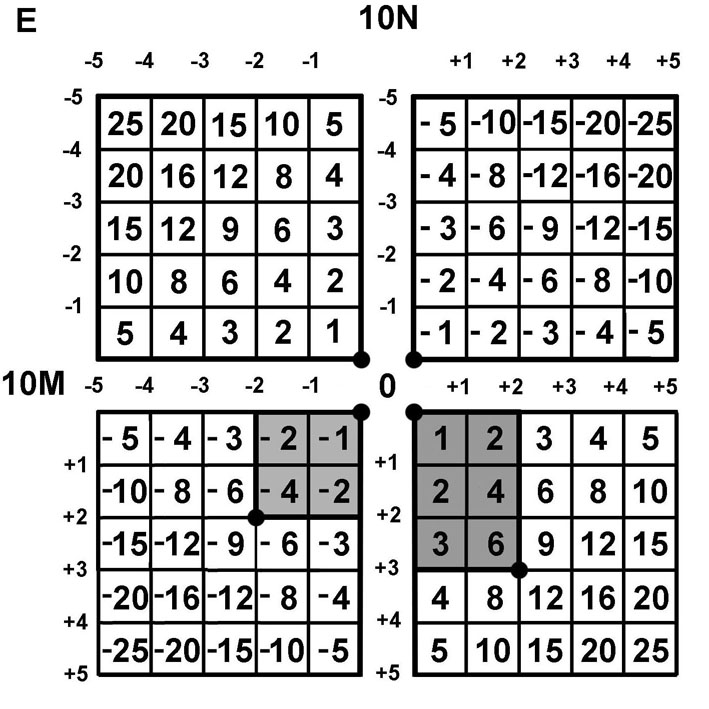
Ищем решение в виде AxB=[D; E], где D -десятки, E - единицы произведения.

Полные десятки - это базовые числа. Линии координат, проходящие через точку (10;10) будем называть базовыми линиями.

Дополнение числа до полного десятка обозначим звездочкой   A*=10-A,   B*=10-B.

Геометрическое построение. На квадрате 10x10 изобразим прямоугольник AxB, отметив точку с координатами (A; B). Дополнительный прямоугольник находится между точками  (A; B)  и  (10; 10).

Разрежем прямоугольник AxB на два прямоугольника той же суммарной площади. Передвигая разрезанные фигуры, получим прямоугольник площади Dx10, одна сторона которого равна десяткам D, и прямоугольник площади E=A*xB*, где E - единицы произведения AxB. (Левая иллюстрация).

Алгоритм "двух камешков" для указания цифр произведения.

На правой базовой координатной линии отмечаем камешком 1 величину множителя A – точка (1) - кружок.

На нижней базовой координатной линии отмечаем камешком 2 величину множителя  B – точка (2) - квадратик.

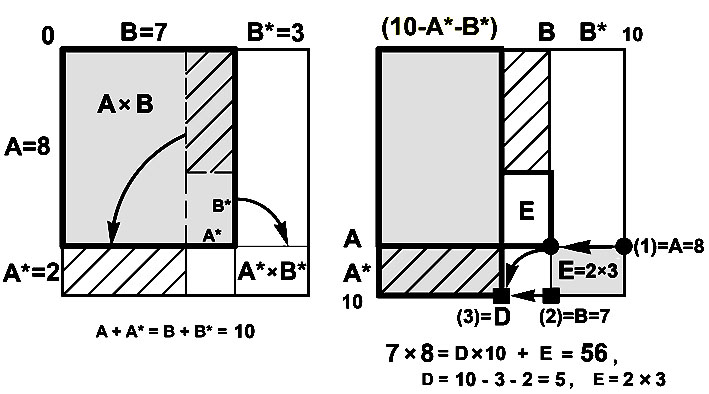
1-й шаг. Перемещаем 1-й камешек A налево на величину B*.

Теперь этот камешек отмечает прямоугольник от точки AxB до точки 10x10,  

его площадь равна числу единиц E=A*xB* произведения AxB.

2-й шаг. Вычитаем из отрезка длины 10 величины A* и B*. Для этого строим окружность с центром во 2-ом камешке радиусом A*.

Перемещаем 2-й камешек из точки (2) налево в точку (3) пересечения окружности и горизонтальной линии.

Длина отрезка от точки (10; 0) до (10; D) равна D = 10 – A* – B*,  где D – число десятков произведения AxB.

В  итоге    D = 10 – A* – B* = A – B*.

Пример.   9 x 9 = ?    A = 9,  B = 9.   A* = 10 – 9 = 1;   B* = 10 – 9 = 1.

Е = A* x B* = 1 x 1 = 1.      D = A – B* = 9 – 1 = 8.  Ответ:  9 x 9 = 10 x 8 + 1 = 81.

Пример.   7 x 8 = ?    A = 7,  B = 8.   A* = 10 – 7 = 3;   B* = 10 – 8 = 2.

Е = A* x B* = 3 x 2 = 6.   D = A – B* = 7 – 2 = 5.  Ответ:  7 x 8 = 10 x 5 + 6 = 56.

"двух   камешков"

для умножения

от 10x10 до 15x15

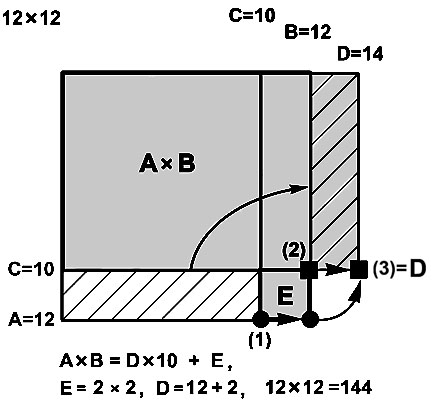
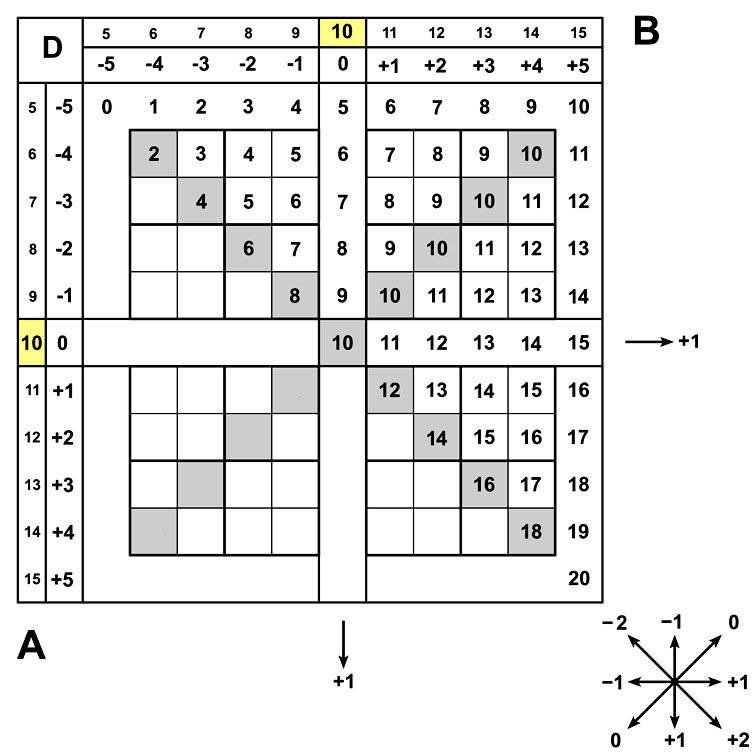
Представим множители X x Y в виде X=(10+A) и Y=(10+B).

На базовых линиях координат отмечаем камешками величины двух множителей:  (10+A) – точка (1) - кружок  и  (10+B) – точка (2) квадратик.

Ищем решение в виде X x Y=[H; D; E].

Для множителей из окрестности базовой точки (10;10) величина сотен H=1.

1-й шаг. Перемещаем 1-й камешек направо на величину B. Теперь этот камешек отмечает модельный прямоугольник от точки 10x10 до точки (10+A)x(10+B).  Число единиц E произведения X x Y равно площади модельного прямоугольника E=AxB.

2-й шаг.  Строим отрезок, длина которого равна сумме  (A + B).

Перемещаем 2-й камешек направо в точку пересечения окружности радиуса A с центром в точке (2) и горизонтальной линии – это точка (3).

Длина отрезка от точки (10; 10) до (10; D) равна   D = A + B,    где D – число десятков произведения X x Y.

Пример.   12x12 = ?  A = 2, B = 2. Е = AxB = 2x2 = 4.   D = A + B = 2 + 2 = 4.  Ответ:  12x12 = [1; 4; 4] = 144.

Для умножения в уме 12x12 достаточно представить в своем воображении модельный квадрат 2x2.

Число единиц E равно площади 2x2. Число десятков равно полупериметру модельного квадрата D=2+2=4.

12x13 = ?  A = 2, B = 3. Е = AxB = 2x3 = 6.   D = A + B = 2 + 3 = 5.  Ответ:  12x13 = [1; 5; 6] = 156.

Для умножения 12x13 минимальный визуальный образ - это модельный прямоугольник 2x3.

Если A£13 и B£13, тогда Е = A*xB* £ 9. Нормализация с переносом «лишних» десятков в старший разряд не требуется. Алгоритм умножения методом пифагоровых схем в диапазоне множителей A£13 и B£13 даёт точные цифры H, D и E.

Подробности см. в статье Творогов В.Б. Как пифагорейцы учили таблицу умножения.

геометрического

 умножения.

Общий случай

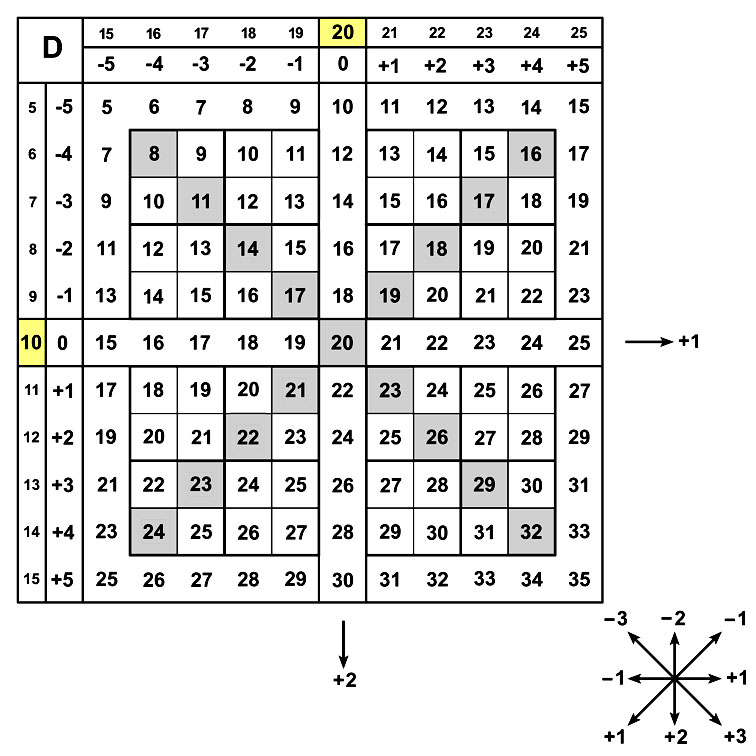
Разность S_A=A–10 между A и базовым числом 10 называется смещением.

Терема. Пусть множители 5 ≤ A ≤ 15;   5 ≤ B ≤ 15. Ищем произведение в виде AxB = [H; D; E].

Тогда   сотни       H = 1;  

             десятки   D = S_A + S_B;  

             единицы  E = S_A x S_B.

На чертеже достаточно иметь прямоугольник со сторонами S_A и S_B. Величина единиц E – это площадь модельного прямоугольника (с учётом знаков смещений), величина десятков D равна полупериметру (сумме двух сторон с учетом знаков смещений).

с базой 10x10

Пример.   13x9= ?  H=1. Множители X=10+3,  Y=10-1.  Смещение A = 3, B = -1. 

Десятки D = A + B = 3 - 1 = 2. Единицы Е = AxB = 3x(-1) = -3.  Ответ:  13x9= [1; 2; -3] = 120 - 3 = 117.

Для умножения 13x9 достаточно представить в воображении прямоугольник 1x3, у которого базовая точка (10;10) находится в левом нижнем углу.

Пример.  14x6 = ?   Сотни H=1. Множители X=10+4,  Y=10-4.  Смещение A = 4, B = -4. 

Десятки D = A + B = 4 - 4 = 0. Единицы Е = AxB = 4x(-4) = -16.  Ответ:  14x6 = [1; 0; (-16)] = 100 - 16 = 84.

Пифагоровы единицы.

Структура не меняется

при смене диапазона

Пифагорова схема

для базы 10x10.

Расчёт десятков

Пифагорова схема

для базы 10x20.

Расчёт десятков

Первый множитель X, близкий к 10, отмечается на вертикальной оси.

Для начальной точки первого приближения удобно взять точку (X; 20). Здесь пифагоровы десятки D = 20 X.

Маршрут решения от (X; 20) до (X; Y) оказывается горизонтальным с кратностью шага 1.

Пример.  12x23 = ?   Множители X = 10+2,  Y = 20+3.  Смещение A = 2, B = 3. 

Начальное приближение для десятков Do = 12x20=24.

пиф-десятки D (12x23) = Do + 3 = 24 + 3 = 27. Единицы Е = AxB = 2x3 = 6.  Ответ:  12x23 = [ (24+3); 6 ] = 276.