Пифагоровы схемы для умножения двузначных чисел

 эффективным счётом

 и быстрым

 визуальным счётом

Эффективным счётом называется устный счёт, который выполняется по оптимальным вычислительным формулам, обеспечивающим наименьшую трудоёмкость. Скорость выполнения вычислителем операций эффективного счёта не принимается во внимание. Человек-вычислитель, воспитанный в традициях стандартной аудиомоторной системы счёта, будет произносить слова о величине обрабатываемых чисел, например, 5x5 может звучать как "пятью пять - двадцать пять".

Быстрым счётом следует называть такие вычисления, которые выполняются человеком с помощью визуальных образов без произнесения слов о величине чисел.

Некоторое количество людей (не более 3%) запоминает таблицы сложения и умножения визуально, как фотографии  "7x8=56" и т.д. Вспоминая таблицу умножения, они как бы достают из хранилища своей памяти фотографии требуемых примеров, и считывают с визуального образа числовые результаты. Эти уникальные люди ведут вычисление так, будто просматривают кинофильм, в котором они записывают расчёты на воображаемой бумаге.  Большинство людей обычных способностей не обладает такими возможностями фотографической памяти.

Визуальная технология счёта доступна для любого человека вполне обычных способностей, так как опирается на элементарные визуальные образы, компактно представляющие математические законы и цифровые правила сокращённых вычислений.

Использование геометрических элементов помогает (1) представить в наглядном виде все арифметические действия, (2) упростить вычисления,  (3) обеспечить высокую скорость решения задачи в уме.

пифагоровой схемы

умножения

(1) Базовое число первого приближения (чаще - это полные сотни, но может быть любой близкий пример с известным ответом);

(2) Пифагоровы десятки как линейные функций от смещений;

(3) Пифагоровы единицы, показанные площадью модельного прямоугольника.

Пусть множители   X = 10 M + S_A,    Y = 10 x N + S_B.  Расчёт с помощью метода пифагоровых схем имеет те же этапы, как и расчёт по формуле

X x Y =  100 M N  + 10 (N S_A + M S_B)  +  ( S_A S_B ).

Пифагорова схема умножения применяется локально в окрестности базовых чисел (полных десятков). В пифагоровой схеме базовые числа выбираются близкими по величине к множителям, поэтому смещения не превосходят 5, 

 -5 ≤ S_A ≤ 5  и  -5 ≤ S_B ≤ 5.

Координатная плоскость множителей разбивается на квадраты размерами 11x11 с центром в базовых числах. 

(Этап 1). Первое приближение - это произведение базовых десятков H = M x N.

(Этап 2).  Все вычисления, выполняемые методом пифагоровых схем, иллюстрируются в геометрических терминах как перемещение по маршруту на координатной плоскости от базы, где результат известен, до точки, указанной исходными множителями.

Каждый шаг по маршруту рассматривается как этап вычисления, а полученные промежуточные результаты расчётов являются последовательными приближениями к искомому решению.

Пифагоровы десятки вычисляются с учётом количества шагов по маршруту, направления перемещения и кратности каждого шага. Пифагоровы десятки являются линейной функцией от величины смещений.

Для конкретного вычисления в уме XxY достаточно представить себе модельный прямоугольник пифагоровых единиц размерами от 1x1 до 5x5. Минимальный визуальный образ состоит только из тех точек и линий, по которым проходит маршрут вычисления.

Например, для вычисления в уме 27x29 можно ограничиться геометрической схемой с прямоугольником 3x1. Здесь 27=30-3,  29=30-1. Цифровая запись решения

27x29 = [ (3x3); 3x(-3-1); (-3)x(-1) ] = [ 9; (-12); 3 ] = [ (90-12); 3 ] = [ 78; 3 ] = 783.

(Этап 3). Пифагоровы единицы не зависят от базовых множителей. Их величина определяются смещениями от базы (как положительными, так и отрицательными по знаку). Пифагоровы единицы иллюстрируются модельными прямоугольниками, у которых стороны равны смещениям, а площадь задаёт величину единиц (с учётом знаков смещений). Пифагоровы единицы удаётся представить  запоминающимися геометрическими образами. Так, 2x2=4 - это квадрат, разрезанный на единичные ячейки, 2x3=6 - это прямоугольник со сторонами 2 и 3 и площадью 6=3+3. 

Если базовые числа выбраны так, что смещения велики (более 5 по абсолютной величине), то они относятся к специальным пифагоровым схемам с большими отклонениями. (Для базовых чисел 50 и 100 такие схемы могут быть эффективными).

* * *

Пифагоровы схемы реализуют эффективные методы визуального счёта с формулами расчётов минимальной трудоёмкости.

Все этапы ментальных вычислений иллюстрируются на пифагоровых схемах геометрическими элементами, что позволяет отказаться от словесных высказываний о величинах промежуточных чисел.

Опираясь на опыт педагогов, которые применяли в практике обучения школьников элементы наглядной арифметики, можно утверждать, что в практике обучения общие описания алгоритма расчёта должны быть конкретизированы для фиксированных значений базовых чисел. Пифагоровы схемы следует изучать для каждого конкретного диапазона, конкретных базовых чисел. Визуальные образы с точными числовыми значениями обрабатываются в визуальной памяти быстрее, чем общие буквенные формулы. Ситуацию можно сравнить с набором карт местности: даже зная о местности общие сведения, мы получаем из конкретной локальной карты существенно больше информации, больше деталей, больше связей и подсказок..

Пифагорова схема

для базы 20x20

На координатной плоскости выделяем квадрат 11 строк и 11 столбцов диапазона от 15 до 25. Центр выделенного квадрата занимает пара множителей 20x20.

Пусть X и Y множители в диапазоне от 15 до 25. Представим множители в виде базового числа и смещения

X=20+A,   Y=20+B.  Здесь -5 ≤ A ≤ 5,   -5 ≤ B ≤ 5.

Общий алгоритм умножения чисел в окрестности множителей 20x20 имеет следующую цифровую запись

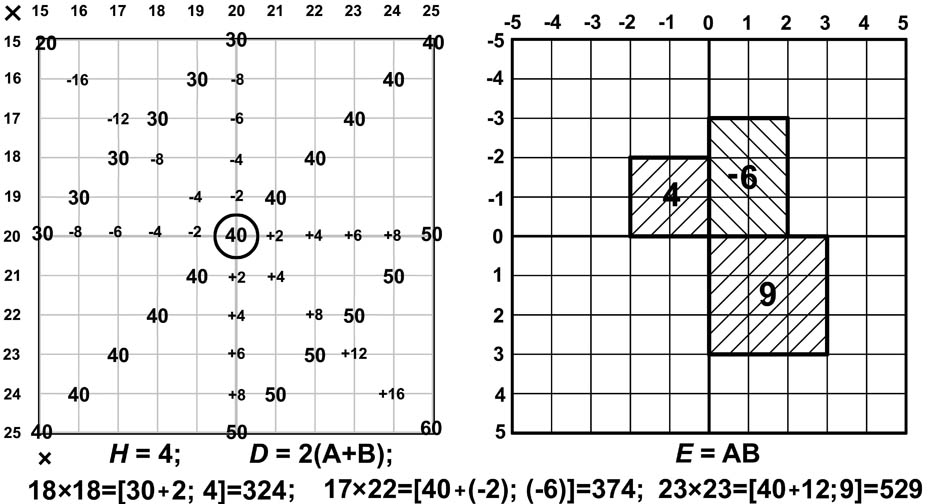
X x Y = [ 2; A ] x [ 2; B ] = [ H; D; E ] = [ (2x2); 2x(A+B); (AxB) ] = [ 4; 2x(A+B); (AxB) ].

Величину в разряде десятков D = 2x(A+B) назовём пифагоровыми десятками. Для базы 20x20 пифагоровы десятки D  равны периметру модельного прямоугольника со сторонами A и B (с учётом знаков).

Величину в разряде единиц E= (AxB) будем называть пифагоровыми единицами. Произведение AxB показываем как площадь модельного прямоугольника со сторонами A и B (с учётом знаков).

Пифагоровы единицы E могут принимать значения от -25 до +25.

Алгоритм, описывающий способ применения пифагоровой схемы, выделяет три этапа.

(1)  Подготовительный этап - приведение множителей к базе и определение рабочих коэффициентов,

(2)  Вычислительный этап  расчёта пифагоровых десятков.

(3)  Завершающий этап. Добавление пифагоровых единиц и нормализация ответа.

На подготовительном этапе фиксируем базовые числа, в данном случае 20x20.

Определяем величину сотен в центральной точке H = 2x2 = 4.

Вычисляем смещения множителей  S_A  = X - 20   и   S_B = Y - 20   от точки 20x20.

Вычислительный этап начинаем с любой точки пифагоровой схемы, где известна величина сотен и десятков, например, в центре 20x20=400.

Величина пифагоровых десятков D равна периметру модельного прямоугольника 2 x (S_A + S_B).

При вычислении пифагоровых десятков мы перемещаемся по маршруту на координатной сетке. Подсчет величины D ведётся с учётом кратности каждого шага (и знака смещения).

Каждый шаг направо увеличивает десятки на 2. Каждый шаг вниз увеличивает десятки на 2. Эти коэффициенты задают кратность шага в заданном направлении.

Разместим на координатной плоскости метки так, чтобы мы могли "с первого взгляда" подсчитать число шагов с учётом кратностей.

Метки - черные кружки - расположены в ячейках. Каждый шаг по маршруту в данную ячейку увеличивает (уменьшает) величину D на число меток в ячейке.

Чтобы различать действия "+1" и "-1" введём понятие антиметки (уменьшающей D на 1). Антиметку будем рисовать как колечко.

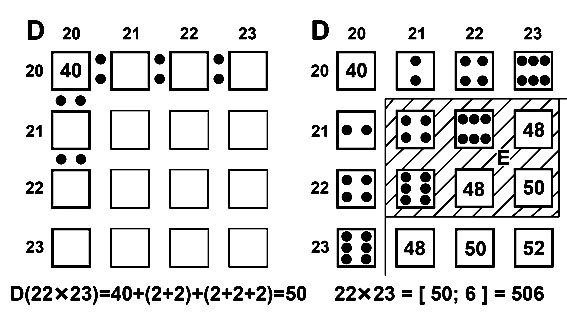
Пример 22 x 23 = ? 

В точке 20x20=400. Базовое число десятков 40.

Перемещаемся на 3 шага направо. Каждый шаг имеет кратность 2. Поэтому прирост D=2x3=6.

Делаем два шага вниз, учитывая кратность 2. Прирост D равен 2x2=4 . Получаем D=6+4=10 -это окончательный ответ для пифагоровых десятков.

Смещение множителя в разложении 22=20+2 равно S_A=2. Смещение второго множителя 23=20+3 равно S_B=3. Поэтому пифагоровы единицы задаются площадью модельного прямоугольника E = S_A x S_B = 2x3 = 6.

Ответ:   22x23 = [ 4; (6+4); (2x3) ] = 400 + 100 + 6 = 506.

 пифагоровых схем -

 шаги по диагонали

Шаг вниз по координатной сетке увеличивает множитель X на 1.

Шаг направо по координатной сетке соответствует увеличению множителя Y на 1.

Если ограничиться только горизонтальными и вертикальными перемещениями, получим эквивалент стандартной схемы поразрядного умножения. 

Между тем, на плоскости у нас есть возможность перемещения по диагоналям - главной и поперечной. На главной диагонали происходит одновременное увеличение множителей при шаге направо вниз

(X;Y)  --> ((X+1);(Y+1)).  При этом кратности вертикального и горизонтального шага складываются.

Шаг вдоль поперечной диагонали направо вверх уменьшает первый множитель и увеличивает второй множитель

(X;Y)  --> ((X-1);(Y+1)).

Полезно запомнить особенности схемы с базой 20x20 : шаг по главной диагонали направо вниз имеет кратность 2+2=4. Шаг вдоль поперечной диагонали направо вверх  имеет кратность 0=2-2.  

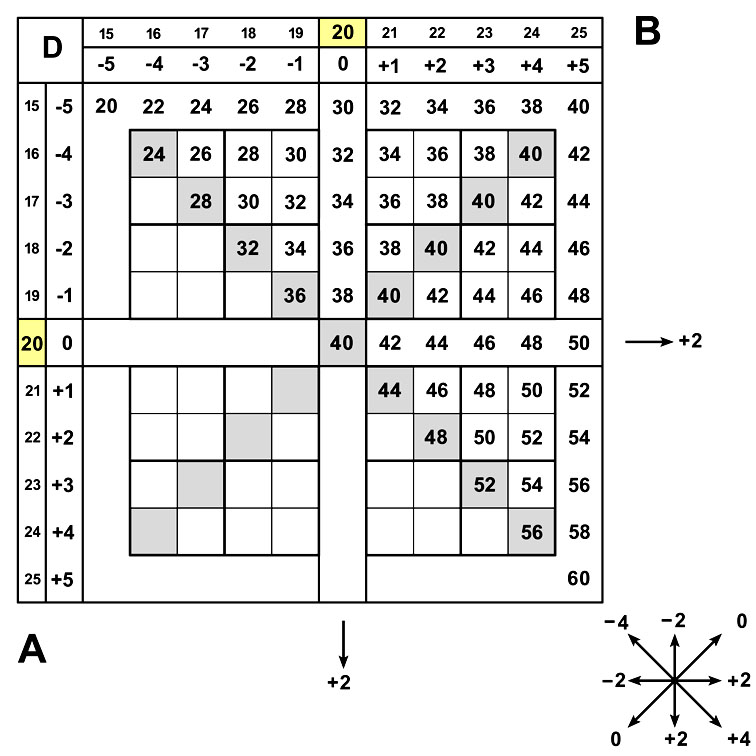
Рассмотрим пифагорову схему с базой (20;20). Здесь в точке 15x15 пиф-десятки D=20.

В точке 15x20 пиф-десятки D=30.

В точке 25x20 пиф-десятки D=40.

Аналогично D(15x20)=30,  D(20x20)=40,  D(25x20)=50,  D(25x25)=60. (Запомним величины десятков в этих мемо-точках).

Пример 1. Вычислим 18x18=? Базовые множители 20x20 указывают разряд сотен H=2x2=4.

От базы (20;20) делаем два шага налево вверх. кратность каждого шага равна (-4). 

18x18 = [ H; D; E ] = [ 4; (-4 -4); (-2)x(-2) ] = [(40 - 8); 4] = [ 32; 4] = 320 + 4 = 324.

Пример 2. Решим пример 17x18. На схеме (20;20) шаг вдоль поперечной диагонали не меняет пиф-десятки (см. рис.)

В самом деле, D(15x20)=30.

30 = D(15x20) = D(16x19) = D(17x18). Поэтому D(17x18) = 30.

Добавляем пифагоровы единицы, равные площади модельного прямоугольника,

17x18 = [ D; E ] = [ 30; (-3)x(-2) ] = 300 + 6 = 306.

 вычислительная

 формула умножения 

для базы 20x20

Пусть множители X и Y  находятся в диапазоне от 15 до 25.

Ищем произведение X x Y в виде  X x Y = [ D; E].  Справедлива эффективная формула

X x Y =  [ 2 ( X + (Y - 20) );  ( S_A x S_B ) ].

Величина 2 (X + (Y - 20) ) = [H; D]  задаёт первые две цифры сотен и десятков произведения.

Затем добавляется величина пифагоровых единиц E = S_A x S_B.

Пример.  17x18=?    17=20-3,   18=20-2.

Величина сотен и десятков [H; D] = 2 ( X + (Y - 20) ) = 2 x { 17 + (18-20) } = 2 x 15 = 30.

Пифагоровы единицы  E =  (-3)x(-2) = 6.   Ответ:  17x18 = [30; 6] = 306.

Для множителей диапазона от 15 до 20 удобно подсчитывать сотни и десятки по формуле 2 x { ( X-10 ) + ( Y-10 ) }.

Цифровая запись решения 17x18= [ 2x(7+8); (-3)x(-2) ] = [ (2x15); 6 ] = [30; 6] = 300 + 6 = 306.

Пример.  22x23=?    22=20+2,   23=20+3.

Величина сотен и десятков [ H; D ] = 2  {22 + (23 - 20 )} = 2 x 25 = 50.

Пифагоровы единицы  E =  2 x 3 = 6.   Ответ:  22 x 23 = [ 50; 6 ] = 506.

Пример.  18x23=?    18=20-2,   23=20+3.

Величина сотен и десятков [ H; D ] = 2 x {18 + (23 - 20 )} = 2 x (21) =  42.

Пифагоровы единицы  E =  (-2)x3 = -6.   Ответ:  18x23 = [42; (-6)] = 414.

 пифагоровых схем

для симметричной базы

[N, 0] x [N, 0]

Для первого приближения в базовой точке вычислим сотни как  H = N N.  

Кратность шага в горизонтальном или вертикальном направлении равна N.

Кратность шага вдоль  главной диагонали равна N + N = 2N.

Кратность шага вдоль  поперечной диагонали равна 0 = N - N.

Алгоритм расчёта для симметричной пифагоровой схемы:

(1) Строим маршрут от базы до точки множителей.

(2) Подсчитываем число шагов L на маршруте в горизонтальном и вертикальном направлении с учетом знака.

(3) Умножаем число шагов на кратность шага. Величина пифагоровых десятков D = L N.

(4) Добавляем пифагоровы единицы. Получаем [H; D; E] = [ (NN);  (LN);  Е ].

Пифагорова схема

для базы 30x30.

Расчёт десятков

Для тренировки навыков умножения с множителями, близкими к 30, можно использовать пифагорову схему следующего вида.

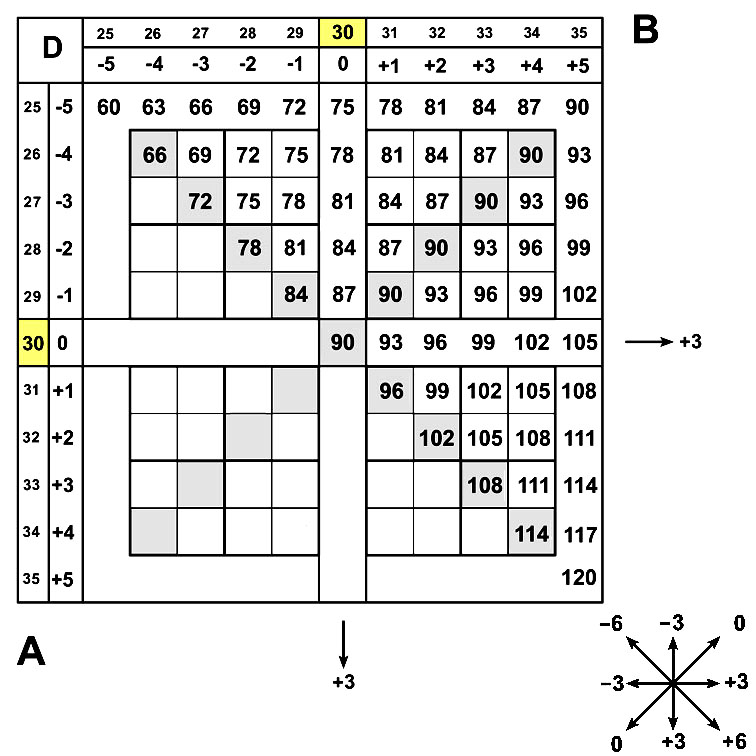
Пример. 28x28 = ?

Маршрут решения выбираем от точки (30x30) до (28x28) два шага налево вверх по главной диагонали с кратностью шага (-6).

Пример. 28x28 = [ 9; (-6 -6); (-2) x (-2) ] = [  (90 - 12);  4 ] = [  78;  4 ] = 784.

 пифагоровых схем.

Общий случай

[M, A] x [N, B]

Выбираем базовые числа 10M и 10N.  

Соглашение № 1. Будем записывать на первом месте младший множитель, на втором месте - большой множитель: M ≤ N. Этот порядок важен для геометрической интерпретации вычислений как перемещений по координатной сетке. Первая координата - вертикальная. Вторая координата - горизонтальная.

При выбранном стандарте M ≤ N направление "направо вверх" приводит к удалению от главной диагонали расширенной таблицы Пифагора. Шаг направо вверх от базы (10M; 10N) всегда приводит к уменьшению величины пифагоровых  десятков.

Допустим, множители приведены к базе   X = 10 M + A,    Y = 10 N + B,     -5 ≤ A ≤ 5  и  -5 ≤ B ≤ 5.

На координатной плоскости множителей выделяем квадрат размерами 11x11 с центром в базовых числах. 

Базовое число первого приближения H = M N.

Расчёт ведётся по формуле

X x Y =  100 M N  + 10 (N A + M B)  +  ( A B ).

Пифагорова схема

для базы 10x30.

Расчёт десятков

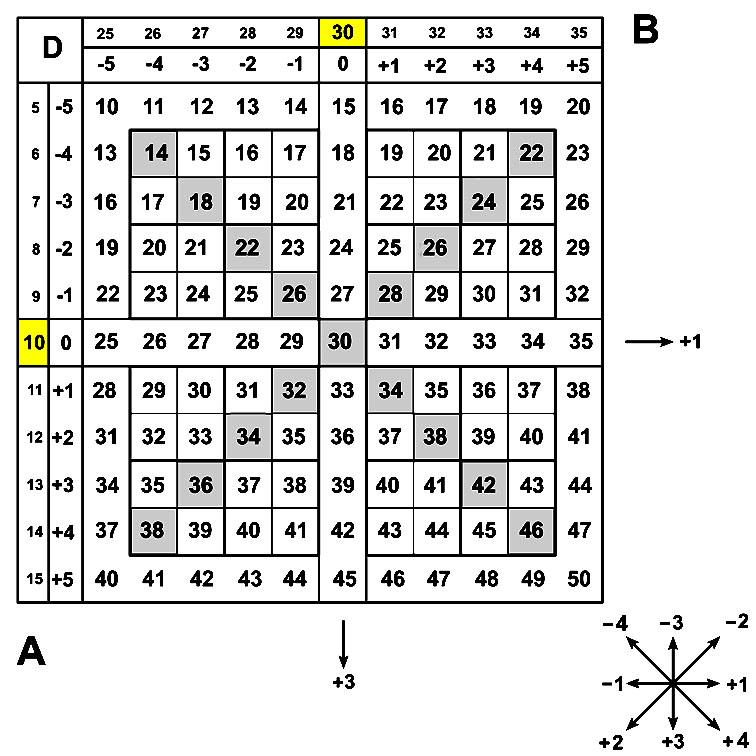
Изучим некоторые особенности  пифагоровой схемы с базой (10; 30).

Прыжок "три шага направо и один шаг вверх" не меняет величины десятков D.  Проверка (+1 +1 +1 -3 = 0).

Прыжок "три шага вниз и один шаг направо" меняют величину десятков D на 10.  Проверка (+3 +3 +3  +1 = 10).

Решая некоторый пример XxY, нужно стараться совершить "прыжок" от базы (10; 30) как можно ближе к точке множителей (X; Y).

Затем за 1-2 шага нужно попасть в точку множителей.

Пример 13x32=?

Выбираем маршрут от базы (10; 30) до (13; 31) как прыжок "три шага вниз и один шаг направо". Прирост десятков +10.

Делаем один шаг направо, добавляем к десяткам еще +1. Получим D(13x32) = D(10x30) + 10 + 1 = 41.

Пифагоровы единицы E (13x32) = 3 x 2 = 6. Ответ   13x32 = [ (30+10+1); (3x2) ] = 416.

Пифагорова схема

для базы 20x30.

Расчёт десятков

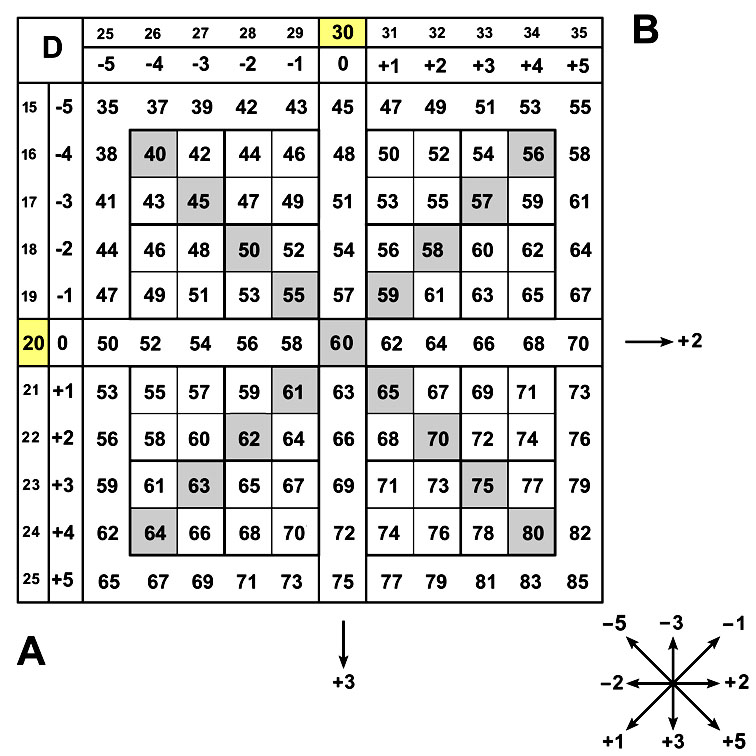
База (20; 30).

Шаг по главной диагонали имеет кратность 5 = 2 + 3.

Два шага по главной диагонали дают прирост пифагоровых десятков 5+5=10 и т.д.

Если точка множителей XxY находится вблизи главной диагонали, нужно перемещаться от базы направо вниз или налево вверх.

Пример 22x32 = [ (2x3);  (5+5) ; (2x2) ] = 600 + 100 + 4 = 704.

Пример 22x28 = ?   Для пиф-схемы (20; 30)  смещения множителей  22 = 20 + 2;  28 = 30 - 2.

Шаг налево вниз  вдоль поперечной диагонали имеет кратность (+1=3-2). (Прирост положительный "+", когда приближаемся к главной диагонали таблицы Пифагора, где множители XxX).

Делаем два шага налево вниз от базы  (20; 30)

22x28 = [ 2x3;  (1 + 1) ; (2x(-2) ] = [ 6;  2; (-4) ] = 620 - 4 = 616.

для базы 40x40.

Пример. 38x38 = ?

От точки (40x40) до (38x38) два шага по главной диагонали налево вверх с кратностью шага (-8).

 38x38 = [ 16; (-8 -8); (-2) x (-2) ] = [  (160 - 16);  4 ] = [  (160 - 20 + 4);  4 ] = 1444.

Пример. 37x38=?   База (40;40). Кратность горизонтального или вертикального шага равна 4.

Маршрут проведём по двум сторонам модельного прямоугольника (-3)x(-2).

H = 4 x 4 = 16. 

D = 4 x ( - 2 - 3) = - 20.

E =  (-3) x (-2) = 6.

Ответ  37x38 = [ 16; (-20); (-3) x (-2) ] = [  (16 - 2);  0;  6 ] = 1406.

Пример. 37x38=?   База (40;40).

Вспомним, что перемещение вдоль поперечной диагонали симметричной схемы не меняет пифагоровы десятки. Здесь один множитель уменьшается, другой множитель увеличивается.

D ( 37 x 38 ) = D ( 36 x 39 ) = D ( 35 x 40 ) = 35 x 2 x 2 =  70 x 2 = 140.

37x38 = [ 140;  (-3) x (-2) ] = [  140;  6 ] = 1406.

умножения чисел до 100

пока не готово

У автора сайта в данный момент нет готовых учебных материалов для тренировки навыков визуального счёта во всех диапазонах до 100 x 100.

Мы объяснили принцип и преимущества пифагоровых схем умножения двузначных чисел. Наши примеры должны были убедить читателей, что геометрические методы во многих случаях упрощают счёт.

Если читатели захотят освоить в совершенстве метод пифагоровых схем, они могут самостоятельно приготовить для себя таблицы пифагоровых десятков для разных базовых чисел и тренироваться с их помощью.