Правила единиц
  На главную страницу

 

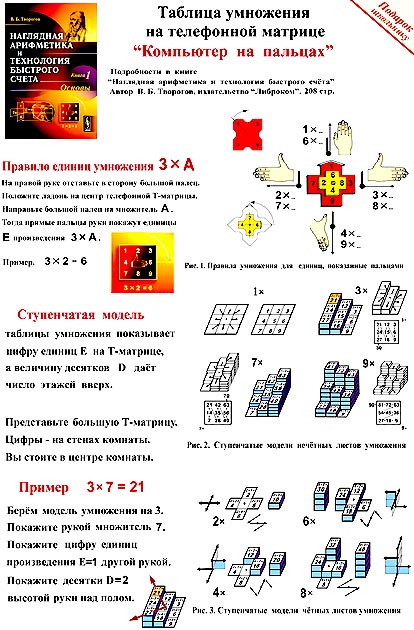
Правила единиц

для таблицы умножения

на телефонной матрице
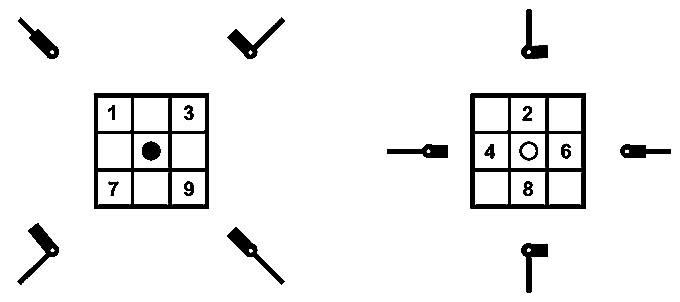
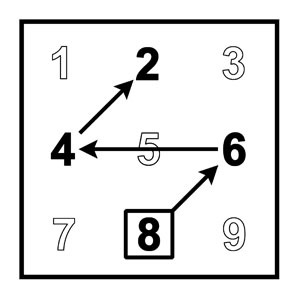
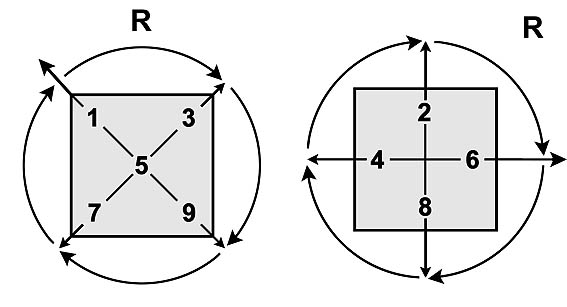
"Галактические" уголки для вычисления единиц E(AxB)

Вершину уголка нужно переместить в центр Т-матрицы и повернуть короткой планкой к цифре A. Тогда длинная планка покажет цифру единиц E соответствующего произведения (см. далее).

Поворот радиального луча на Т-матрице

Обозначим R или R+1  поворот радиального луча на Т-матрице на прямой угол по часовой стрелке.

        Тогда   R ( 1 ) = 3,   R ( 3 ) = 9,   R ( 9 ) = 7,   R ( 7 ) = 1,  

                    R ( 6 ) = 8,   R ( 8 ) = 4,   R ( 4 ) = 2,   R ( 2 ) = 6,  

По определению,    R ( 5 ) = 5,   R ( 0 ) = 0.

Обозначим R 2 поворот радиального луча на Т-матрице на два прямых угла (на 180 градусов).

        Тогда   R 2 ( 1 ) = 9,   R 2 ( 9 ) = 1,   R 2 ( 3 ) = 7,   R 2 ( 7 ) = 3,  

                    R 2 ( 6 ) = 4,   R 2 ( 4 ) = 6,   R 2 ( 2 ) = 8,   R 2 ( 8 ) = 2.  

Обозначим R- 1  поворот радиального луча на Т-матрице на прямой угол против часовой стрелки.

        Тогда   R- 1 ( 1 ) = 7,   R- 1 ( 7 ) = 9,   R- 1 ( 9 ) = 3,   R- 1 ( 3 ) = 1,  

                    R- 1 ( 6 ) = 2,   R- 1 ( 2 ) = 4,   R- 1 ( 4 ) = 8,   R- 1 ( 8 ) = 6.  

Правила единиц для умножения 1, 3, 7, 9  на однозначное число A

  1 x A  =  A Единицы произведения  E ( 1 x A ) совпадают с A.
 E ( 3 x A ) = R ( A ) Единицы произведения  E ( 3 x A ) находятся справа от луча множителя A.
 E ( 7 x A ) = R - 1 ( A ) Единицы произведения  E ( 7 x A ) находятся слева от луча множителя A.
 E ( 9 x A ) = R 2 ( A ) Единицы произведения  E ( 9 x A ) находятся на противоположном луче от множителя A.

Правила единиц для умножения  6, 8, 2, 4 на чётный множитель H Î {2, 4. 6. 8}

E ( 6 x H ) = H Единицы произведения  E ( 6 x H ) совпадают с H.
 E ( 8 x H ) = R ( H ) Единицы произведения  E ( 8 x H ) находятся справа от луча множителя H.
 E ( 2 x H ) = R - 1 ( H ) Единицы произведения  E ( 2 x H ) находятся слева от луча множителя H.
 E ( 4 x H ) = R 2 ( H ) Единицы произведения  E ( 4 x H ) находятся на противоположном луче от множителя H.

* Замечание.  Умножение чётного множителя H на нечётное число A  не может быть выполнено поворотом радиальных лучей Т-матрицы на прямые углы. Правильный ответ для единиц при умножении чёт на нечёт можно получить, если применить коррекцию ±5.

Подробнее см. статью:  Цифровые вертушки как инструмент умножения 

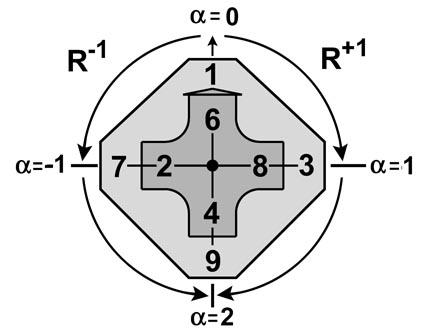
Измерение углов  поворота лучей на Т-матрице
Повороты радиальных лучей Угловая мера числа
 

Умножение на нечётные множители 3, 7, 9

(см. также правила цифровых вертушек)

3-й лист умножения

3-я молния

Правило единиц

умножения на 3

 Компьютер "на пальцах" 3xA Правило единиц 3xA
     

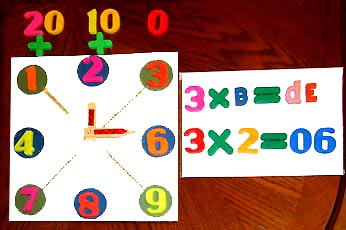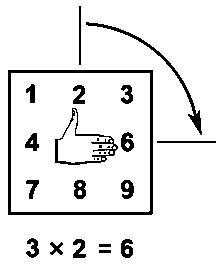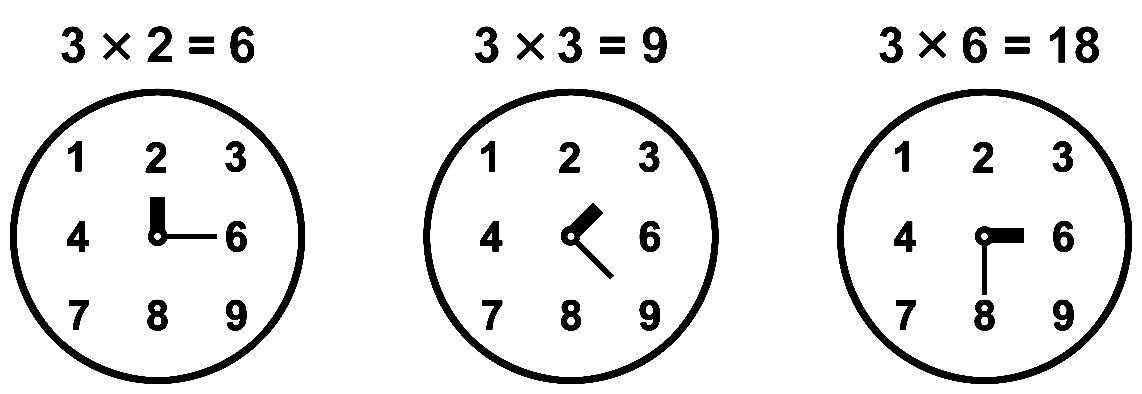7-й лист умножения

Примеры 7xA

Компьютер "на пальцах" 7xA

  
 

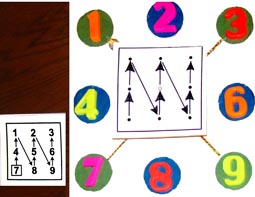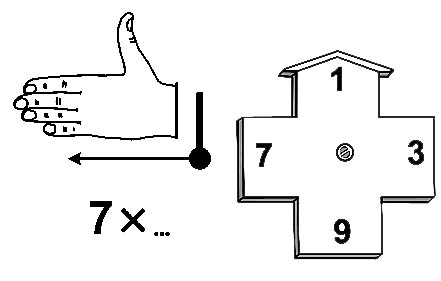9-й лист умножения
9-я молния и цифровые правила  9xA  

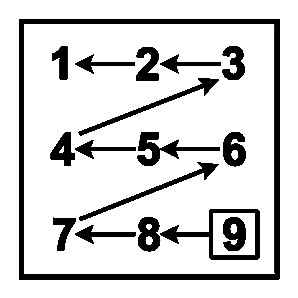9xA = [(A - 1), (A*)]

A* = 10 - A

 

 
 

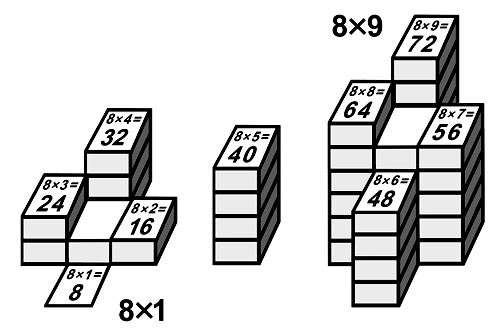
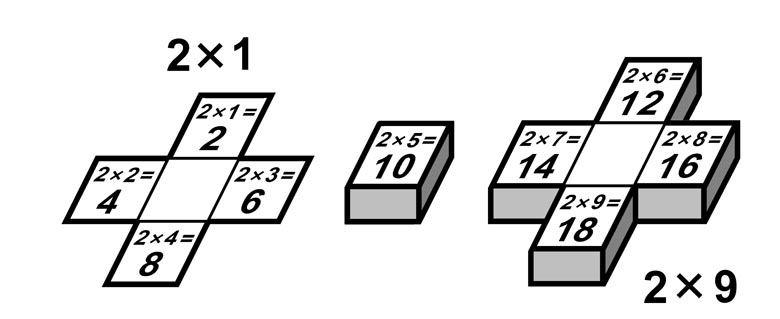
Умножение на чётные множители 2, 4, 6, 8

легко выполняется на ступенчатых моделях листов умножения

с помощью поворота чётной молнии
2-й лист умножения

2-я молния и ступенчатая модель

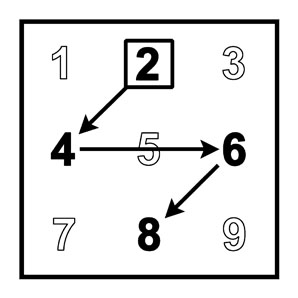(A < 5)   D = 0.        (A >= 5)  D = 1.
4-й лист умножения

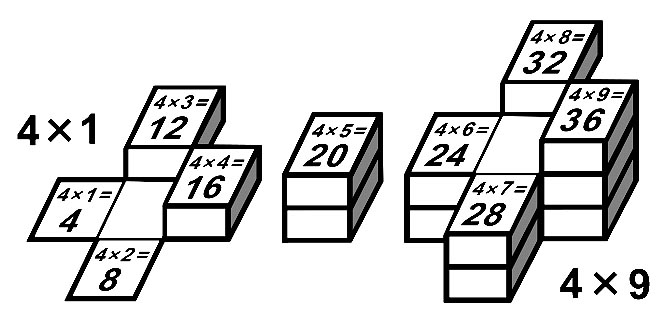
4-й лист умножения и ступенчатая модель

  
 
6-й лист умножения

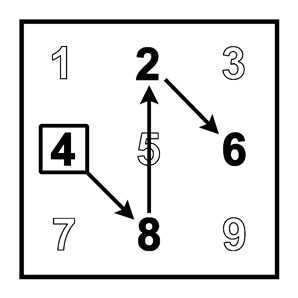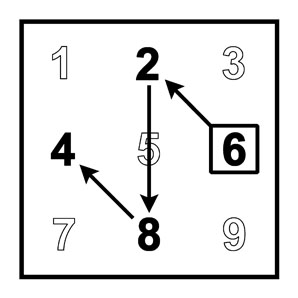
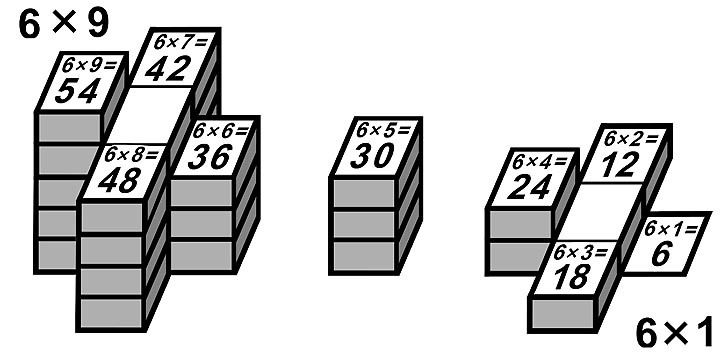
6-я молния и ступенчатая модель 6xA

  
 
8-й лист умножения

8-я молния и ступенчатая модель 8xA

 Правило десятков 8xA  

    A = { 1, 2, 3, 4, 5 }

         D = A - 1.

 

    A = { 6, 7, 8, 9 }

         D = A - 2.

 		  

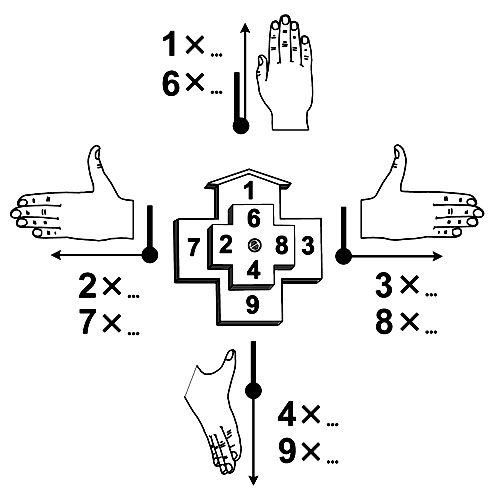
"Компьютер

на пальцах"

Правило единиц
Ладонь - инструмент вычисления

Ладонь кладём на центр Т-матрицы.

Поворачиваем ладонь большим пальцем к множителю A.

 Рука - указатель цифр произведения AxB=[D;E].

Рука показывает единицы как радиальные лучи Т-матрицы.

Высота руки над основанием показывает десятки произведения.

Тот же файл высоко разрешения 4,5 Mb

См. подробнее статью: "Компьютер на пальцах" в игровом методе изучения таблицы умножения
 
На главную страницу