|
Определения |
|
|
На главную страницу |
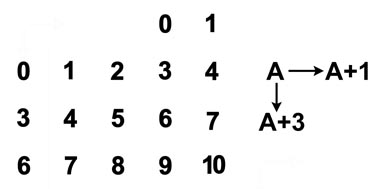
Стандарт Т-матрицы
для устного счёта
В требованиях стандарта Т-матрицы для устного счета предполагается, что человек, изучающий визуальную технологию быстрого счёта, должен уметь решать две взаимосвязанные задачи.
1) По заданному однозначному числу A нужно быстро определять место расположения числа A на Т-матрице.
2) По заданной ячейке Т-матрицы нужно быстро определять число A, находящееся в этой ячейке.
Например, для числа 3 эти требования стандарта Т-матрицы означают, что правый верхний угол Т-матрицы и число 3 для человека-вычислителя ассоциируются как тождественные визуальные образы.
Конфигурации для чисел
Числовая плоскость
Цифровая плоскость
Т-матрица
| Т-матрица. | Числовая плоскость | Элементы Т-матрицы | |
 |
|
 |
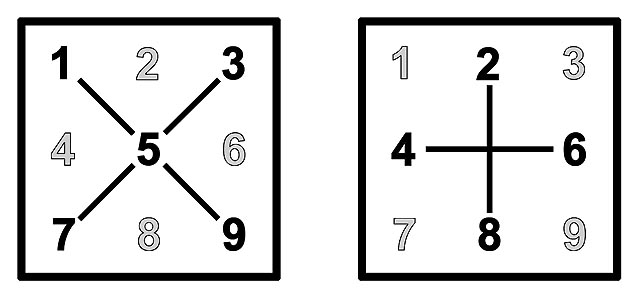Продолжение (текст): Различные конфигурации
Цифровое правило - это алгоритм, который позволяет получить цифру ответа проще, чем математическое определение.
Вычислительная формула - это алгебраическая формула для вычисления конкретной цифры произведения (десятков или единиц).
|
Базовые примеры |
Для базовых примеров ответ может быть получен простыми схемами или цифровыми правилами.
Базовые примеры составляют часть таблицы умножения. Остальные примеры умножения решаются общими правилами указания цифр.
Чтобы умножить число A на 10, нужно записать число A в разряд десятков, а 0 записать в разряд единиц
10 x A = [ A, 0 ].
9 x A = [ (A - 1), A* ], где дополнение A* = 10 - A.
Десятки D на единицу меньше множителя A. Единицы E равны дополнению множителя A* = 10 - A.
|
9 x 2 = [ (2-1), 2* ] = 18 9 x 3 = [ (3-1), 3* ] = 27 9 x 4 = [ (4-1), 4* ] = 36 9 x 5 = [ (5-1), 5* ] = 45 |
9 x 6 = [ (6-1), 6* ] = 54 9 x 7 = [ (7-1), 7* ] = 63 9 x 8 = [ (8-1), 8* ] = 72 9 x 9 = [ (9-1), 9* ] = 81 |
Умножение
9 x A
|
9 x A = [D; E] D = A - 1 E = 10 - A |
 |
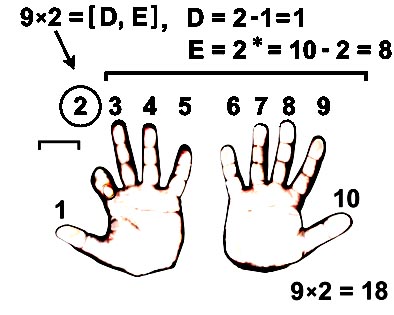* Это правило умножения полезно для детей, начинающих изучение арифметики.
Умножение
A x B,
если A и B больше 5.
|
Пронумеруем пальцы от 6 до 10. Соединим пальцы A и B.
Умножение "на пальцах" 7 x 8
D = сумма "нижних" пальцев = 2+3 = 5 E = произведение "верхних" пальцев левой и правой руки = 3 x 2 = 6 |
 |
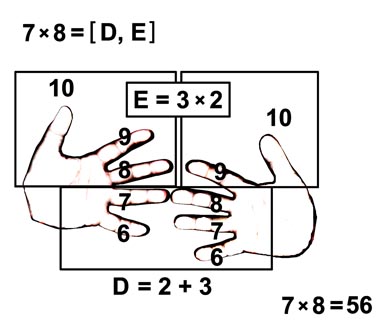* Это правило умножения полезно для детей, начинающих изучение арифметики.
6 x А
|
6 x A = [ (A/2), A ],
где A = { 2, 4, 6, 8 }
|
6x2=[(2/2);
2]= 10+2 =12 6x4=[(4/2); 4]= 20+4 =24 6x6=[(6/2); 6]= 30+6 =36 6x8=[(8/2); 8]= 40+8 =48 |
 |
4 x А
|
1 вариант |
2 вариант |
||
|
4 x A = [ (A/2), (-A)] где A = { 2, 4, 6, 8 } |
4x2=[(2/2);(-2)]=
10-2 = 8 4x4=[(4/2);(-4)]= 20-4 =16 4x6=[(6/2);(-6)]= 30-6 =24 4x8=[(8/2);(-8)]= 40-8 =32 |
4 x A = [ (A/2-1), A*]
где A = { 2, 4, 6, 8 }
А* = 10 - A |
4x2=[(2/2-1);
2*]= 0 +8 = 8 4x4=[(4/2-1); 4*]= 10+6 =16 4x6=[(6/2-1); 6*]= 20+4 =24 4x8=[(8/2-1); 8*]= 30+2 =32 |
9 x A
на Т-матрице
|
9 x 1 = 09, 9 x 4 = 36,
9 x 2 = 18, 9 x 9 = 81
9 x 3 = 27, 9 x 8 = 72
9 x 5 = 45, 9 x 6 = 54 |
 |
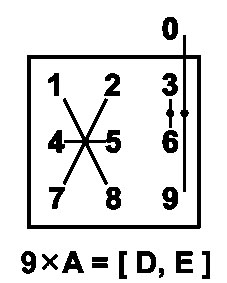(1) Находим
D = A - 1. Десятки на единицу меньше множителя. (2) Линия, начинающаяся в D, указывает цифру E на Т-матрице D --> E = 9 - D |
5 x A
|
5 x A = [ (A/2), 0 ]
10 / 2 = 5
|
 |
(1) Берем парную симметричную конфигурацию для
A (2) Разрезаем конфигурацию по линии симметрии (3) Число десятков D - это число целых меток. Если есть разрезанная метка, то E = 5. |
|
A - четный множитель,
5 x 2 = [ (2/2), 0 ] = 10 5 x 4 = [ (4/2), 0 ] = 20 5 x 6 = [ (6/2), 0 ] = 30 5 x 8 = [ (8/2), 0 ] = 40 |
A - нечетный множитель. Половина десятка [ (1/2), 0 ] = 5. 5 x 3 = [ (3/2), 0 ] = [ (1 + 1/2), 0 ] = 15 5 x 5 = [ (5/2), 0 ] = [ (2 + 1/2), 0 ] = 25 5 x 7 = [ (7/2), 0 ] = [ (3 + 1/2), 0 ] = 35 5 x 9 = [ (9/2), 0 ] = [ (4 + 1/2), 0 ] = 45 |