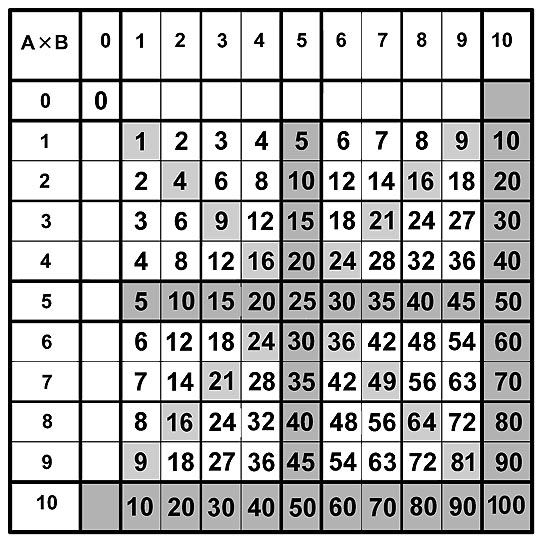
Наглядная арифметика -

 это раздел математики,

 который изучает

арифметику

 средствами геометрии. 

Сайт готов к использованию   Продолжается разработка

Update 18.12.2013

       Здесь представлена информация о технологии быстрого счета.

       Наш сайт помогает преодолеть заблуждения обывателя об устном счете. Каждому человеку необходимо знать, что :

(1) Методы устного счета, использующие геометрические схемы, отличаются от методов вычислений на бумаге.

(2) Слова, которые человек произносит при счёте, замедляют вычислительную работу. Самый высокую скорость даёт технология  визуального счета, в которой геометрические картинки, возникающие в памяти, подсказывают числовые ответы.

(3) Правила единиц и правила десятков указывают цифры произведения AxB = [D; E] непосредственно по величине множителей A и B.

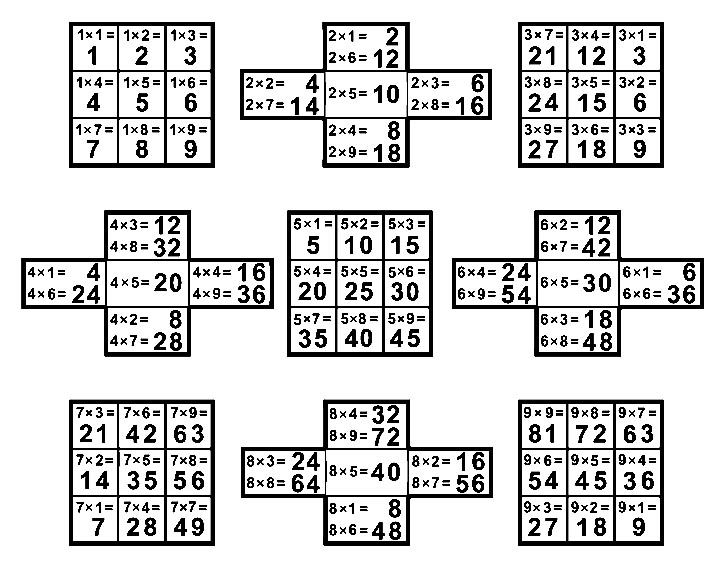
(4) Таблица умножения Пифагора имеет линейный вид. Можно изобразить другую таблицу умножения в виде девяти листов размерами 3x3 - девятилистник умножения.

(5)  Цифровые вертушки используют телефонную Т-матрицу как экран. При поворотах пропеллера вертушки появляются отдельные листы умножения, на которых видны все ответы примеров с одинаковыми первыми множителями.

(6)  Вращающаяся таблица умножения представляет собой вариант цифровой вертушки, на которой одновременно видны единицы и  десятки результатов умножения. Зная цифровые правила вращающейся таблицы умножения, не нужно учить примеры умножения в виде словесных фраз.

(7) "Компьютер на пальцах" - это способ указания руками цифр результатов умножения на  телефонной Т-матрице и ступенчатой модели. Руками можно показать не только конкретные числа ответов арифметических примеров, но и правила умножения на заданные множители.

   Издана книга В. Б. Творогов  "Наглядная арифметика и технология быстрого счета". Книга 1. Основы. - М., изд. URSS. - 2011, 205 с.

   Вторая книга этой серии, посвященная умножению двузначных чисел, предположительно, выйдет во второй половине 2014 года. Некоторые методы умножения двузначных чисел приведены далее.

   Литература о наглядной арифметике будет включена в наш обзор по мере появления публикаций.

   Автор имеет несколько патентов РФ. Среди изобретений имеются вращающаяся таблица умножения, цифровые вертушки. О них рассказывается далее.

"...Способность, необыкновенно ценная для всех."  ( Л. Н. Толстой )     (о тесной связи устного счета и мышления)

Заучивая примеры таблицы умножения в виде фраз «Дважды два – четыре», мы используем аудиомоторную технологию устного счёта, в которой все числа и действия с ними озвучиваются словами. Скорость такого устного счёта крайне медленная. Однако возможности человека не являются столь ограниченными. Известны феномены людей – супервычислителей, которые демонстрировали перед публикой образцы скоростного устного счёта, поражающего воображение. Процесс их вычислений реализуется на основе визуальной памяти человека, без произнесения слов.  Продолжение...

Почему мы считаем медленно?

Виды технологий устного счёта

Наглядная арифметика

как раздел математики -

предмет и содержание

Что уничтожили вики-инквизиторы, стерев статью о наглядной арифметике? Наглядная арифметика показывает нам структуру таблицы умножения, которая во всех деталях аналогична вращению планет вокруг солнца. Повторим крылатую фразу: "А все-таки она вертится!", которая приписывается астроному, физику и механику Галилео Галилею (1564-1642).

Уничтожить ссылки на планетарную модель таблицы умножения "нео-инквизиторы от вики", конечно, могут. И уничтожают, не заботясь о том, что будут думать о них окружающие.

Но уничтожить планетарную модель, заложенную природой в нашу таблицу умножения, "нео-инквизиторам от вики" не удастся ни при каких обстоятельствах. Каждый грамотный человек должен знать - числа в таблице умножения тоже вертятся!

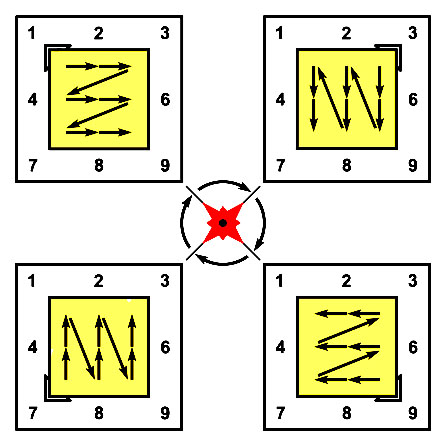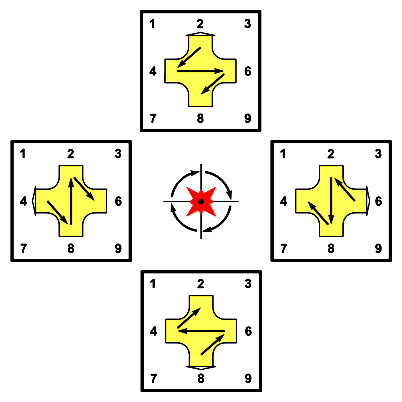См. далее: девятилистник сложения и девятилистник умножения

Надеемся, что энтузиасты, понявшие преимущества визуальной технологии счёта, сумеют преодолеть искусственный барьер на пути к аудитории интернета, возникший по недоумию и скудознанию некоторых администраторов. Полезно было бы разместить информацию на своих сайтах, не подверженных цензуре.

*   *   *

Термин "наглядная арифметика" или "визуальная арифметика" рассматривается как раздел математики, изучающий арифметику средствами геометрии. Предметом изучения наглядной арифметики является технология устного счёта. Цель наглядной арифметики - предложить  с помощью геометрических схем и визуальных образов  алгоритмы решения арифметических задач, максимально возможной эффективности.

Вычислительный процесс, происходящий в голове человека, исследуется на основе принципов визуализации (геометризации) всех элементов.

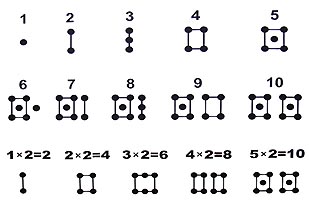
Человек воспринимает количество как множество элементов. Упорядоченное конечное множество называется конфигурацией. Самый удобный способ обработки конфигураций - придание им геометрической формы. Квадраты, прямоугольники, симметричные фигуры - это основной материал для визуального счёта с малыми количествами элементов.

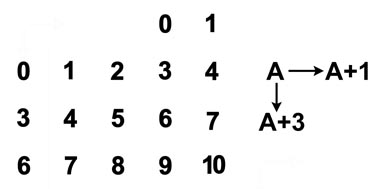
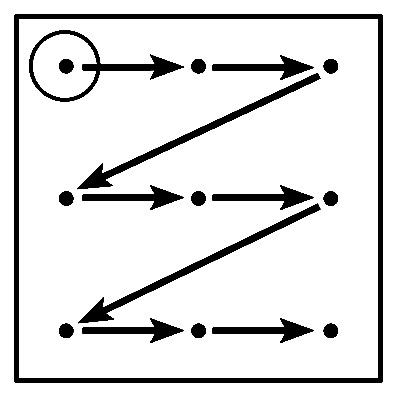
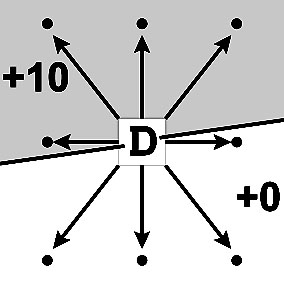
Чтобы разные люди могли понимать друг друга и использовать одинаковые геометрические схемы для одних и тех же действий, в наглядной арифметике принимается стандарт числовой линии и стандарт телефонной Т-матрицы для устного счёта. (Зеркальная Т*-матрица никогда не используется). Т-матрица является частью числовой плоскости, на которой шаг направо соответствует увеличению числа "+1", шаг вниз увеличивает число по правилу "+3".

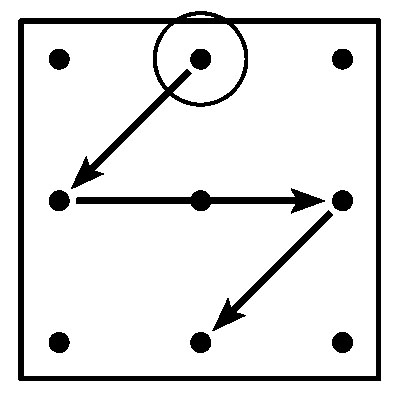
Для подсказки чисел ответа применяются стрелочки-указатели. Решить арифметический пример и представить себе направление указателя ответа, ведущего от исходной цифры к результату - это один и тот же процесс.

Для эффективной системы счёта нужны средства сокращённых вычислений, реализуемые, в вычислительных формулах. Чтобы умножить на Ax10, нужно приписать к числу A нуль справа. Это - самая известная и полезная цифровая формула. В наглядной арифметике формулы сокращённых вычислений есть для всех элементарных случаев сложения или умножения.

Статья "Наглядная арифметика" для электронной энциклопедии.

   Основы визуального счета. Конфигурации - это фиксированные расположения элементов.

В устном счёте используются конфигурации - на линии "по 1", "по 2", "по 3", "по 5". 

Принцип визуализации вычислений. Векторы - указатели цифр ответов.

Цифровые вертушки.   Продолжение...

  Сложение. Сложение на числовой линии и числовой плоскости. Т-матрица. Молния Т-матрицы. Указатели.

Цифровые правила десятков и единиц. Геометрические методы быстрого сложения.  Продолжение...

Молния +1	Молния +2	Указатель	Инверсия	Молния +3	Молния +7

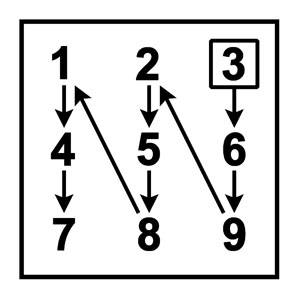
Таблица умножения Пифагора

* Лист умножения вытянут в линию

* Лист умножения представлен матрицей 3x3

однозначных чисел

  Базовые примеры умножения. Для базовых примеров умножения существуют специальные упрощенные алгоритмы указания ответов.  Умножение на 10 и 5. Умножение на 9. Умножение на 6.  Продолжение...

  Правила единиц. Как получить из множителей цифру единиц произведения?  Продолжение...

  Правила десятков. Схемы для указания величины десятков произведения. Продолжение...

  Девятилистник умножения.  Цифровые вертушки. Симметричный вид таблицы умножения. Продолжение...

 "Компьютер на пальцах". Простые способы указания цифр ответов руками. Продолжение...

двузначных чисел

 Геометрическое умножение. Алгоритм "двух камешков" показывает ответы до 15x15. База (10;10) и (10;20). Продолжение...

 Умножение двузначных чисел на пифагоровых схемах. База (20;20), (30;30), (20;30), (10;30),. Продолжение...

 Пространство множителей и пространство решений на пифагоровых схемах. База (20;20), (30;30). Статья

 Мемо-точки в устном умножении двузначных чисел.  Статья

 Возведение двузначного числа в квадрат. Эффективные алгоритмы и геометрические подсказки.  Статья

 Квадрат двузначного числа на телефонной матрице. Цифровые вертушки для квадратов чисел.  Статья

 Геометрические симметрии как способ упрощения вычислений.  Статья

Часто задаваемые вопросы

    Стандартная (пифагорова) арифметика основана на навыках счета с помощью загибания пальцев. Таблица умножения традиционно заучивается словами типа "дважды два - четыре". Это приводит к медленному и трудному процессу устного счета.

    Зная о свойствах  цифровых и геометрических правил арифметики, устный счет можно превратить в легкий, быстрый и приятный процесс умственной работы, почти мгновенно дающий числовые ответы.

    В математике нужно доказывать все утверждения и цифровые правила. Теоретические разделы наглядной арифметики должны осваивать школьники, знакомые с основами алгебры.

Обсуждения

  Оказывается, взаимные повороты двух телефонных Т-матриц позволяют прочитать среди возникающих комбинаций цифр все ответы умножения однозначных чисел. Продолжение...

"Число есть сущность всех вещей, и организация Вселенной в ее определениях представляет собой вообще гармоническую систему чисел и их отношений». Пифагор. - Эпиграф статьи "Магия чисел в науке и природе", Лоскович М.В., Натяганов В.Л., Слепова Т.В. (2000 г.)

Гостевая книга на данном сайте  N-ARIFMETIKA.NAROD.RU

Замечания, мнения и предложения по наглядной арифметике

просьба высылать по е-адресу N-ARIFMETIKA@YANDEX.RU